![]()

![]()
![]()

![]()
Problem: Given a complete undirected graph G=(V, E) that has nonnegative integer cost c(u, v) associated with each edge (u, v) in E, the problem is to find a hamiltonian cycle (tour) of G with minimum cost.
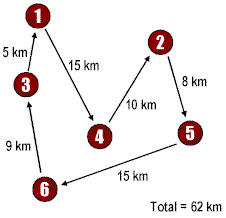
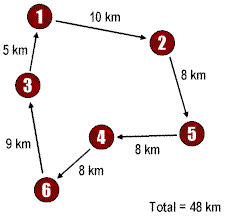
A salespersons starts from the city 1 and has to visit six cities (1 through 6) and must come back to the starting city i.e., 1. The first route (left side) 1→ 4 → 2 → 5 → 6 → 3 → 1 with the total length of 62 km, is a relevant selection but is not the best solution. The second route (right side) 1 → 2 → 5 → 4 → 6 → 3 → 1 represents the must better solution as the total distance, 48 km, is less than for the first route.
Suppose c(A) denoted the total cost of the edges in the subset A subset of E i.e.,
c(A) = ∑u,v in A c(u, v)
Moreover, the cost function satisfies the triangle inequality. That is, for all vertices u, v, w in V, w have c(u, w) ≤ c(u, v) + c(v, w).
Note that the TSP problem is NP-complete even if we require that the cost function satisfies the triangle inequality. This means that it is unlikely that we can find a polynomial-time algorithm for TSP.
When the cost function satisfies the triangle inequality, we can design an approximate algorithm for TSP that returns a tour whose cost is not more than twice the cost of an optimal tour.
First, compute a MST (minimum spanning tree) whose weight is a lower bound on the length of an optimal TSP tour. Then, use MST to build a tour whose cost is no more than twice that of MST's weight as long as the cost function satisfies triangle inequality.
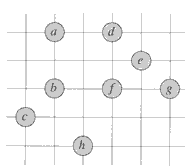
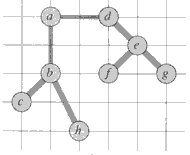
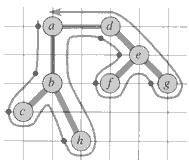
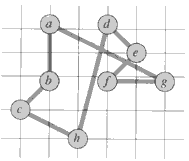
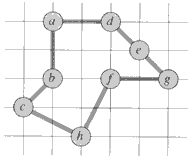
which is about 23% shorter.
Theorem: APPROX-TSP-TOUR is a polynomial-time 2-approximation algorithm for TSP with triangle inequality.
Proof:
1. We have already shown that APPROX-TSP-TOUR-time.
2. Let H* denote the optimal tour. Observe that a TSP with one edge removed is a spanning tree (not necessarily MST).
It implies that the weight of the MST T is in lower bound on the cost of
an optimal tour.
c(T) = c(H*)
A "Full" walk, W, traverse every edge of MST, T, exactly twice. That is,
c(w) = 2c(T)
which means
c(w) ≤ 2c(H*)
and we have
c(w)/c(H*)
≤ p(n) = 2
That is, the cost of walk, c(w), of the solution produced by the algorithm is within a factor of p(n)=2 of the cost c(H*) of an optimal solution. □
Without the triangle inequality, a polynomial time approximate algorithm with constant approximation ratio not exist unless P=NP.
Theorem: If P ≠ NP, there is no polynomial-time algorithm with approximation ratio p≥1 for general TSP.
Proof:
Suppose to the contrary that there exists a polynomial-time algorithm A for p≥1.
Now, use algorithm A to solve instance of HAM-CYCLE problem in polynomial-time. Since HAM-CYCLE problem is NP-complete then by theorem
If any NP-complete problem is polynomial-time solvable, then P=NP. Equivalently, if any problem in NP is not polynomial-time solvable than no NP-complete problem is polynomial solvable.
Solving HAM-CYCLE in polynomial-time implies that P=NP.
Since the HAM-CYCLE is NP-complete and we assumed and we assumed that P≠NP, a contradiction is arise. □
Let G = (V, E) be an instance of Hamiltonian cycle problem. We want to determine efficiently whether G contains a Hamiltonian cycle by making use of an algorithm A. We transform G into an instance of the TSP problem as follows:
Consider a complete graph G`=(V, E`) where E` = {(u, v): u, v in V and u≠v}. Assign an integer cost to each edge in E` as follows:
c(u,v) = 1 if (u, v) in E P|V| + 1 otherwise
Because algorithm A is guaranteed to return a tour of cost no more than P times the cost of an optimal tour, if graph G contains a Hamiltonian cycle, then A must return it. If G has no Hamiltonian cycle, then A returns a tour of cost more than P|V|. Therefore, we can use algorithm A to solve Hamiltonian cycle problem in polynomial time and this is impossible unless P=NP.