The chain matrix multiplication problem is perhaps the most popular example of dynamic programming used in the upper undergraduate course (or review basic issues of dynamic programming in advanced algorithm's class).

The chain matrix multiplication problem involves the question of determining the optimal sequence for performing a series of operations. This general class of problem is important in complier design for code optimization and in databases for query optimization. We will study the problem in a very restricted instance, where the dynamic programming issues are clear. Suppose that our problem is to multiply a chain of n matrices A₁ A₂ ... A_n. Recall (from your discrete structures course), matrix multiplication is an associative but not a commutative operation. This means that you are free to parenthesize the above multiplication however we like, but we are not free to rearrange the order of the matrices. Also, recall that when two (non-square) matrices are being multiplied, there are restrictions on the dimensions.

Suppose, matrix A has p rows and q columns i.e., the dimension of matrix A is p × q. You can multiply a matrix A of p × q dimensions times a matrix B of dimensions q × r, and the result will be a matrix C with dimensions p × r. That is, you can multiply two matrices if they are compatible: the number of columns of A must equal the number of rows of B.

In particular, for 1 ≤ i ≤  p and 1 ≤ j ≤ r, we have

C[i, j] = ∑_{1 ≤ k ≤ q} A[i, k] B[k, j].

There are p . r total entries in C and each takes O(q) time to compute, thus the total time to multiply these two matrices is dominated by the number of scalar multiplication, which is p . q . r.

Problem Formulation

Note that although we can use any legal parenthesization, which will lead to a valid result. But, not all parenthesizations involve the same number of operations. To understand this point, consider the problem of a chain A₁, A₂, A₃ of three matrices and suppose

A₁ be of dimension 10 × 100
A₂ be of dimension 100 × 5
A₃ be of dimension 5 × 50

Then,

MultCost[((A₁ A₂) A₃)] = (10 . 100 . 5) +  (10 . 5 . 50) = 7,500 scalar multiplications.

MultCost[(A₁ (A₂ A₃))] = (100 . 5 . 50) + (10 . 100 . 50) = 75,000 scalar multiplications.

It is easy to see that even for this small example, computing the product according to first parenthesization is 10 times faster.

The Chain Matrix Multiplication Problem

Given a sequence of n matrices A₁, A₂, ... A_n, and their dimensions p₀, p₁, p₂, ..., p_n, where where i = 1, 2, ..., n, matrix A_i has dimension p_{i − 1} × p_i, determine the order of multiplication that minimizes the the number of scalar multiplications.

Equivalent formulation (perhaps more easy to work with!)

Given n matrices, A₁, A₂, ... A_n, where for 1 ≤ i ≤ n, A_i is a p_{i − 1} × p_i, matrix, parenthesize the product A₁, A₂, ... A_n so as to minimize the total cost, assuming that the cost of multiplying an p_{i − 1}× p_i matrix by a p_i × p_{i + 1} matrix using the naive algorithm is p_{i − 1}× p_i × p_{i + 1}.

Note that this algorithm does not perform the multiplications, it just figures out the best order in which to perform the multiplication operations.

Naive Algorithm

Well, lets start from the obvious! Suppose we are given a list of n matrices. lets attack the problem with brute-force and try all possible parenthesizations. It is easy to see that the number of ways of parenthesizing an expression is very large. For instance, if you have just one item in the list, then there is only one way to parenthesize. Similarly, if you have n item in the list, then there are n − 1 places where you could split the list with the outermost pair of parentheses, namely just after first item, just after the second item, and so on and so forth, and just after the (n − 1)^th item in the list.

On the other hand, when we split the given list just after the k^th item, we create two sublists to be parenthesized, one with k items, and the other with n − k items. After splitting, we could consider all the ways of parenthesizing these sublists (brute force in action). If there are L ways to parenthesize the left sublist and R ways to parenthesize the right sublist and since these are independent choices, then the total is L times R. This suggests the following recurrence for P(n), the number of different ways of parenthesizing n items:

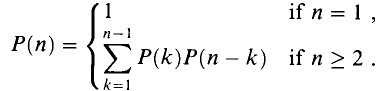
This recurrence is related to a famous function in combinatorics called the Catalan numbers, which in turn is related to the number of different binary trees on n nodes. The solution to this recurrence is the sequence of Catalan numbers. In particular P(n) = C(n − 1), where C(n) is the n^th Catalan number. And, by applying Stirling's formula, we get the lower bound on the sequence. That is,

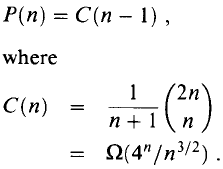
since 4ⁿ is exponential and n^3/2 is just a polynomial, the exponential will dominate the expression, implying that function grows very fast. Thus, the number of solutions is exponential in n, and the brute-force method of exhaustive search is a poor strategy for determining the optimal parenthesization of a matrix chain. Therefore, the naive algorithm will not be practical except for very small n.

Dynamic Programming Approach

The first step of the dynamic programming paradigm is to characterize the structure of an optimal solution. For the chain matrix problem, like other dynamic programming problems, involves determining the optimal structure (in this case, a parenthesization). We would like to break the problem into subproblems, whose solutions can be combined to obtain a solution to the global problem.

For convenience, let us adopt the notation A_{i .. j}, where i ≤ j, for the result from evaluating the product  A_i A_{i + 1} ... A_j. That is,

A_{i .. j} ≡ A_i A_{i + 1} ... A_j ,    where i ≤ j,

It is easy to see that is a matrix A_{i .. j}  is of dimensions p_i × p_{i + 1}.

In parenthesizing the expression, we can consider the highest level of parenthesization. At this level we are simply multiplying two matrices together. That is, for any k, 1 ≤  k ≤  n − 1,

A_1..n = A_1..k  A_k+1..n .

Therefore, the problem of determining the optimal sequence of multiplications is broken up into two questions:

Question 1: How do we decide where to split the chain? (What is k?)   

Question 2: How do we parenthesize the subchains A_1..k  A_k+1..n?

The subchain problems can be solved by recursively applying the same scheme. On the other hand, to determine the best value of k, we will consider all possible values of k, and pick the best of them. Notice that this problem satisfies the principle of optimality, because once we decide to break the sequence into the product , we should compute each subsequence optimally. That is, for the global problem to be solved optimally, the subproblems must be solved optimally as well.

The key observation is that the parenthesization of the "prefix" subchain A_1..k within this optimal parenthesization of A_1..n. must be an optimal parenthesization of A_1..k.

Dynamic Programming Formulation

The second step of the dynamic programming paradigm is to define the value of an optimal solution recursively in terms of the optimal solutions to subproblems. To help us keep track of solutions to subproblems, we will use a table, and build the table in a bottom­up manner. For 1 ≤ i ≤ j ≤ n, let m[i, j] be the minimum number of scalar multiplications needed to compute the A_i..j. The optimum cost can be described by the following recursive formulation.

Basis: Observe that if i = j then the problem is trivial; the sequence contains only one matrix, and so the cost is 0. (In other words, there is nothing to multiply.) Thus,

m[i, i] = 0 for i = 1, 2, ..., n.

Step: If i ≠ j, then we are asking about the product of the subchain A_i..j and we take advantage of the structure of an optimal solution. We assume that the optimal parenthesization splits the product, A_i..j into for each value of k, 1 ≤  k ≤  n − 1 as A_i..k . A_k+1..j.

The optimum time to compute is m[i, k], and the optimum time to compute is m[k + 1, j]. We may assume that these values have been computed previously and stored in our array. Since A_i..k is a matrix, and A_k+1..j is a matrix, the time to multiply them is p_{i − 1} . p_k . p_j. This suggests the following recursive rule for computing m[i, j].

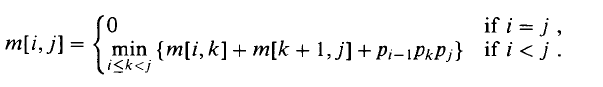
To keep track of optimal subsolutions, we store the value of k in a table s[i, j]. Recall, k is the place at which we split the product A_i..j to get an optimal parenthesization. That is,

s[i, j] = k such that m[i, j] = m[i, k] + m[k + 1, j] + p_{i − 1} . p_k . p_j.

Implementing the Rule

The third step of the dynamic programming paradigm is to construct the value of an optimal solution in a bottom-up fashion. It is pretty straight forward to translate the above recurrence into a procedure. As we have remarked in the introduction that the dynamic programming is nothing but the fancy name for divide-and-conquer with a table. But here in dynamic programming, as opposed to divide-and-conquer, we solve subproblems sequentially. It means the trick here is to solve them in the right order so that whenever the solution to a subproblem is needed, it is already available in the table.

Consequently, in our problem the only tricky part is arranging the order in which to compute the values (so that it is readily available when we need it). In the process of computing m[i, j] we will need to access values m[i, k] and m[k + 1, j] for each value of k lying between i and j. This suggests that we should organize our computation according to the number of matrices in the subchain. So, lets work on the subchain:

Let L = j − i + 1 denote the length of the subchain being multiplied. The subchains of length 1 (m[i, i]) are trivial. Then we build up by computing the subchains of length 2, 3, ..., n. The final answer is m[1, n].

Now set up the loop: Observe that if a subchain of length L starts at position i, then j = i + L − 1. Since, we would like to keep j in bounds, this means we want j ≤ n, this, in turn, means that we want i + L − 1 ≤ n, actually what we are saying here is that we want i ≤ n − L +1. This gives us the closed interval for i. So our loop for i runs from 1 to n − L + 1.

Matrix-Chain(array p[1 .. n], int n) {
          Array s[1 .. n − 1, 2 .. n];
          FOR i = 1 TO n DO m[i, i] = 0;                                         // initialize
          FOR L = 2 TO n DO {                                                      // L=length of subchain
                  FOR i = 1 TO n − L + 1 do {
                           j = i + L − 1;
                          m[i, j] = infinity;
                          FOR k = i TO j − 1 DO {                                  // check all splits
                                  q = m[i, k] + m[k + 1, j] + p[i − 1] p[k] p[j];
                                  IF (q < m[i, j]) {
                                          m[i, j] = q;
                                           s[i, j] = k;
                                  }
                           }
                   }
            }
           return m[1, n](final cost) and s (splitting markers);
           }

Example [on page 337 in CLRS]: The m-table computed by MatrixChain procedure for n = 6 matrices A₁, A₂, A₃, A₄, A₅, A₆ and their dimensions 30, 35, 15, 5, 10, 20, 25.

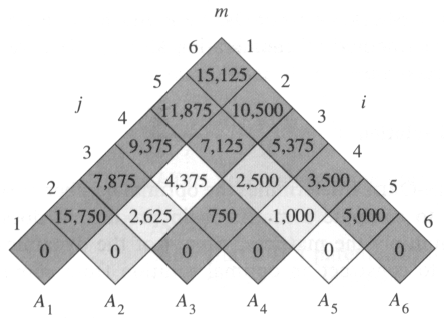
Note that the m-table is rotated so that the main diagonal runs horizontally. Only the main diagonal and upper triangle is used.

Complexity Analysis

Clearly, the space complexity of this procedure Ο(n²). Since the tables m and s require Ο(n²) space. As far as the time complexity is concern, a simple inspection of the for-loop(s) structures gives us a running time of the procedure. Since, the three for-loops are nested three deep, and each one of them iterates at most n times (that is to say indices L, i, and j takes on at most n − 1 values). Therefore, The running time of this procedure is Ο(n³).

Extracting Optimum Sequence

This is Step 4 of the dynamic programming paradigm in which we construct an optimal solution from computed information. The array s[i, j] can be used to extract the actual sequence. The basic idea is to keep a split marker in s[i, j] that indicates what is the best split, that is, what value of k leads to the minimum value of m[i, j]. s[i, j] = k tells us that the best way to multiply the subchain is to first multiply the subchain A_i..k and then multiply the subchain  A_k+1..j, and finally multiply these two subchains together. Intuitively, s[i, j] tells us what multiplication to perform last. Note that we only need to store s[i, j] when we have at least two matrices, that is, if j > i. The actual multiplication algorithm uses the s[i, j] value to determine how to split the current sequence. Assume that the matrices are stored in an array of matrices A[1..n], and that s[i, j] is global to this recursive procedure. The procedure returns a matrix.

Mult(i, j) {
       if (i = = j) return A[i];            // Basis
       else {
                   k = s[i, j];
                   X = Mult(i, k];          // X=A[i]…A[k]
                   Y = Mult(k + 1, j];     // Y=A[k+1]…A[j]
                    return XY;               // multiply matrices X and Y
              }
        }

In the example, the procedure computes the chain matrix product according to the parenthesization ((A₁(A₂ A₃))((A₄ A₅) A₆).

Recursive Implementation

Here we will implement the recurrence  in the following recursive procedure that determines m[i, j], the minimum number of scalar multiplications needed to compute the chain matrix product Ai..j. The recursive formulation have been set up in a top-down manner. Now consider the following recursive implementation of the chain­matrix multiplication algorithm. The call Rec­Matrix­Chain(p, i, j) computes and returns the value of m[i, j]. The initial call is Rec­Matrix­Chain(p, 1, n). We only consider the cost here.

Rec-Matrix-Chain(array p, int i, int j) {
      if (i = = j) m[i, i] = 0;                               // basic case
      else {
                  m[i, j] = infinity;                          // initialize
                  for k = i to j − 1 do {                   // try all possible splits
                           cost=Rec-Matrix-Chain(p, i, k) + Rec-Matrix-Chain(p, k + 1, j) + p[i − 1]*p[k]*p[j];
                           if (cost<m[i, j]) then
                                    m[i, j]= cost;
                           }
                   }                                               // update if better
       return m[i,j];                                          // return final cost
}

This version, which is based directly on the recurrence (the recursive formulation that we gave for chain matrix problem) seems much simpler. So, what is wrong with this? The answer is the running time is much higher than the algorithm that we gave before. In fact, we will see that its running time is exponential in n, which is unacceptably slow.

Let T(n) be the running time of this algorithm on a sequence of matrices of length n, where n = j − i + 1.

If i = j, then we have a sequence of length 1, and the time is Θ(1). Otherwise, we do Θ(1) work and then consider all possible ways of splitting the sequence of length n into two sequences, one of length k and the other of length n − k, and invoke the procedure recursively on each one. So, we get the following recurrence, defined for n ≥ 1.

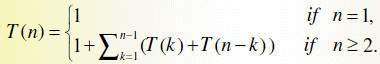
Note that we have replaced the Θ(1)'s with the constant 1.

Claim: T(n) = 2^{n − 1}.

Proof. We shall prove by induction on n. This is trivially true for n = 1. (Since T(1) ≥ 1 = 2⁰.) Our induction hypothesis is that T(m) = 2^{m − 1}. for all m < n. Using this hypothesis, we have

T(n) = 1 + ∑_{1≤ k≤ n-1} (T(k) + T(n − k))

≥ 1 + ∑_{1≤ k≤ n-1} T(k)                      -- Ignore the term T(n − k).

≥ 1 + ∑_{1≤ k≤ n-1} (2^{k −1})                  -- by application of induction hypothesis.

= 1 + ∑_{0≤ k≤ n-2} (2^k)                      -- By application of geometric series formula.

= 1 + (2^{n −1} + 1)

= 2^{n −1}.

 Therefore, we have T(n) = Ω(2ⁿ).

Now the question is why this is so inefficient than that of bottom-up dynamic programming algorithm? If you "unravel'' the recursive calls on a reasonably long example, you will see that the procedure is called repeatedly with the same arguments. The bottom-up version evaluates each entry exactly once.

Memoization [I think this should be Memorization but lets stick to the textbook!]

Now from very practical viewpoint, we would like to have the nice top-down structure of recursive algorithm with the efficiency of bottom-up dynamic programming algorithm. The question is: is it possible? The answer is yes, using the technique called memoization.

The fact that our recursive algorithm runs in exponential time is simply due to the spectacular redundancy in the number of time it issues recursive calls. Now our problem is how could we eliminate all this redundancy? We could store the value of "cost" in a globally accessible place the first time we compute it and then simply use this precomputed value in place of all future recursive calls. This technique of saving values that have already been computed is referred to as memoization.

The idea is as follow. Let's reconsider the function Rec­Matrix­Chain() given above. It's job is to compute m[i, j], and return its value. The main problem with the procedure is that it recomputes the same entries over and over. So, we will fix this by allowing the procedure to compute each entry exactly once. One way to do this is to initialize every entry to some special value (e.g. UNDEFINED). Once an entries value has been computed, it is never recomputed.

In essence, what we are doing here is we are maintaining a table with subproblem solution (like dynamic programming algorithm), but filling up the table more like recursive algorithm. In other words, we would like to have best of both worlds!

Mem-Matrix-Chain(array p, int i, int j) {
         if (m[i, j] != UNDEFINED) then
                   return m[i, j];                            // already defined
         else if ( i = = j) then
                      m[i, i] = 0;                                // basic case
                else {
                         m[i, j] = infinity;                    // initialize
                         for k = i to j − 1 do {               // try all splits
                               cost = Mem-Matrix-Chain(p, i, k) + Mem-Matrix-Chain(p, k + 1, j) + p[i − 1] p[k] p[j];
                               if (cost < m[i, j]) then      // update if better
                                   m[i, j] = cost;
                               }
                        }
         return m[i, j];                                      // return final cost
}

Like the dynamic programming algorithm, this version runs in time Ο(n³). Intuitively, the reason is this: when we see the subroblem for the first time, we compute its solution and store in the table. After that whenever we see the subproblem again, we simply looked up in the table and returned the solution. So, we are computing each of the Ο(n²) table entry once and, and the work needed to compute one table entry (most of it in the for­loop) is at most Ο(n). So, memoization turns an Ω(2ⁿ)-time algorithm into an time Ο(n³)-algorithm.

As a matter of fact, in general, Memoization is slower than bottom-up method, so it is not usually used in practice. However, in some dynamic programming problems, many of the table entries are simply not needed, and so bottom-up computation may compute entries that are never needed. In these cases, we use memoization to compute the table entry once. If you know that most of the table will not be needed, here is a way to save space. Rather than storing the whole table explicitly as an array, you can store the "defined" entries of the table in a hash table, using the index pair (i, j) as the hash key.

See Chapter 11 in CLRS for more information on hashing.