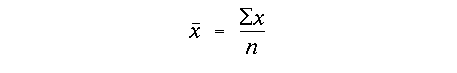
Introduction
Measurements systems
Random variables
Parametric vs. non parametric methods
Central tendencies, mean, and variance
Accuracy vs. Precision

Lord Kelvin:

            "... when you can measure what you are speaking about and express
            it in numbers, you know something about it; but when you cannot
            express it in numbers, your knowledge is of a meagre and
            unsatisfactory kind; it may be the beginning of knowledge, but you
            have scarcely in your thoughts advanced to the state of science,
            whatever the matter may be."

Mark Twain (paraphrased):

         "There are three types of untruths: Lies, damn lies, and statistics!"

Clearly, the true utility of a quantitative approach lies somewhere between these two extremes. Lord Kelvin in his certainty of a "Clockwork Universe" either did not appreciate the magnitude of uncertainty and random error in the real world, or dismissed its importance.  Mark Twain's quote is humorous because it acknowledges our distrust of that which we may not understand or which we perceive as indefinite.

In contrast, in the real world statistics are at worst, a necessary evil, and at best a powerful tool for dealing with the randomness and uncertainty that is inherent in any system of measurement.  Statistical methods provide us with a means of classifying data, comparing data, generating quantitative, testable hypotheses, and assessing the significance of an experimental or observational result.

Why do we need or use statistics?

1.  Data reduction
        Example: Analysis of very large satellite data sets

2. Inference (assess levels of uncertainty or differences between samples)
        Example: Water quality testing - Is a well dangerously contaminated?

3. Quantify relationships between variables
        Example:  Explore the atmospheric CO₂ - climate linkage

There are several systems of measurement that we may encounter.

Nominal - the nominal scale compares properties in a qualitative or very simple quantitative way.  For example we may define the occurrence of a microfossil as present or absent in a particular stratum, or we may classify rocks as igneous, metamorphic or sedimentary.

Ordinal - Once placed on a nominal scale, we may want to define some property of an object in a more comprehensive way using an ordinal scale with discrete, pre-determined steps. We could rank the abundance of one taxa of microfossil in a sample as: absent, rare, common, very common, or abundant. Abundance on the ordinal scale can be represented by the integers 1-5 or 0-4. Or we could rank the hardness of a mineral from 1 to 10 using Moh's hardness scale.  Workers in the Social Sciences make extensive use of ordinal values on the Likert scale for dealing with survey data (e.g. Strongly Agree, Somewhat Agree, Agree, Disagree, Somewhat Disagree, Strongly Disagree).  One potential drawback of the ordinal scale is that the discrete levels are not necessarily evenly spaced.  For example, how we perceive the difference between "strongly agree" and "somewhat agree" likely varies from person to person. This poses difficulty for analytical or statistical treatment of the data. One approach to dealing with this type of data is the use of non-parametric, or distribution-free statistical methods. These will be discussed later in the course.

Continuous data can be broken down into two subclasses -

Interval - The simplest of the truly quantitative or continuous measurement scales - the interval scale - is anchored at an arbitrary reference or zero point, but increasing or decreasing measurements are divided into equally spaced intervals.  For example, the Celsius temperature scale places zero degrees at the freezing point of water, an arbitrary, but convenient convention. Parametric, or distribution-based statistical methods can be used with data measured on the interval scale.

Ratio - Properties measured on the ratio scale are also continuous, but are tied to an absolute reference point. Physical properties such as length, volume, velocity and time fall into this category.  Measurements of variables on the ratio scale are inherently quantitative and can be manipulated numerically, analytically, or statistically.

Variables describe the properties of an object or population. If we measure a variable in a fair or unbiased way, and for example, have no means of knowing the specific outcome of the measure before it is conducted, the variable is said to be random.

If we measure repeatedly from a single population, we draw a random sample from that population. Any quantity computed from repeated samples of a random variable is a statistic. It is important to differentiate between population parameters and sample statistics. If we could measure a random variable "x" infinitely, we would be able to determine its true or expected value, denoted E(x), or ⟨x⟩.  In practice, we can only collect a small number of observations or samples from the entire population of the random variable, and thus must rely on statistics calculated from subsamples of the entire population to infer the properties of the underlying population from which the samples are drawn. This introduces errors or uncertainty which we seek to quantify through statistical tests.

Random variables are extremely important in statistics.  One of the fundamental assumptions behind many statistical methods is that the data used to conduct the test represents a random sample of a random variable. If the data is systematically biased, this basic assumption is violated, and the statistical theory behind the test is not appropriate. Any conclusions drawn from such a test are compromised and suspect.

The first basic statistical assumption deals with randomness. The second assumption deals with the likelihood of a particular response or outcome that a random variable may exhibit. The frequency of a particular observed outcome (often called a successful outcome) in some number n measurements of a random variable is referred to as the probability of that outcome. Due to many sources of uncertainty, a random variable can have a range of possible outcomes.  Suppose we made an infinite number of observations of a random variable. If we then plotted the frequency of each outcome as a function of the observed value, we would in general, obtain a smooth curve with a central peak that decreased towards higher and lower values (called the tails of the distribution). This curve is called the probability distribution function for the random variable. It can have a number of particular types of shapes, some of which will be discussed later.

If a statistical test depends on or is sensitive to the probability distribution function (or PDF) of a random variable, it is said to be a Parametric or distribution-based method.  If the method is applicable regardless of the shape of the underlying PDF of the random variable, the method is said to be a non-parametric or distribution-free method.

Perhaps the most basic measure of a random variable is its central tendency.  There are several ways in which this can be assessed.  The simplest is the mode, which is defined as the maximum number of occurrence of a particular value within the PDF.  A second measure is the median.  The median is defined as the value in the PDF for which half of the remaining values are smaller and half are larger.  This measure is fairly insensitive to outliers, values with unusually large errors.

The most important measure however of the central tendency of a random variable is the mean, which is defined as:

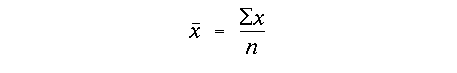
where the x with an overbar is the symbol used to define the mean and the Greek sigma symbol (∑) denotes the sum of all n values of x. One of the reasons that the mean is so important statistically is because in the limit as n goes to infinity, the expected value of a random variable is the mean. A simple way to think about this is that if n is very, very large, the random errors will cancel, leaving the true value of the random variable, the population mean.

Knowledge of the mean is important, but does not fully define the shape of the PDF. It is useful to know how much variability exists around the mean.  An easy way to do this is to calculate the range, the distance between the minimum and maximum observed values. In most cases, however this is unsatisfactory because the range can be quite large and is very sensitive to random errors due to extreme outliers. As a better way to assess the variability about the sample mean, we can define the unbiased sample variance as the sum of squares of individual deviations from the mean as follows:

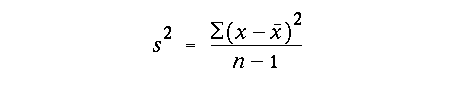
We'll discuss these important statistics for describing the PDF of a random variable - the sample mean and variance - more in class.

In the real world, several factors contribute to variability in a random variable.  These include natural variability ("signal") and error ("noise").  Errors can arise from the way in which a sample is collected and handled ("sampling errors"), or from the method or device used to measure the sample ("measurement errors").

Noise places limits on the accuracy (systematic bias) and precision (random bias) of a measurement.

Accuracy assesses the systematic bias in a measurement.  A measurement that is accurate provides a good estimate of the expected value of a random variable from repeated measurements. Note however, that an accurate measurement my exhibit random bias and thus may be imprecise.

Precision assesses the reproducibility or random bias in a measurement.  A measurement that is precise can be reproduced with little variability.  Such a measurement could however be systematically biased, and thus inaccurate.

Univariate Statistical Terms

Here are some statistical terms that you will encounter.  Can you describe them in your own words?

Systems of measurement
     Nominal
     Ordinal
     Interval
     Ratio
Random variables
    Population parameters
    Expected values
    Samples
    Sample Statistics
Frequency distribution of a random variable
     Shape
     Central tendencies
          mode
          median
          mean
     Variance and standard deviation
Normal distribution and z-scores