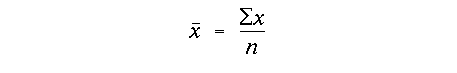
Introduction
Central Limit Theorem
Degrees of Freedom

Generalized Procedure for Statistical Hypothesis Testing
Z-test (large sample mean test)
One-Sample Student's t-test (small sample mean test)

Paired Student's t-test (small sample test for a difference between non-independent paired means)

Two-sample Student's t-test (small sample test for a difference between two independent means)

Type I and Type II errors in hypothesis testing

We have already introduced the concept of the frequency distribution for a random variable.  If we divide each bin in the frequency distribution by N, the total number of samples collected, then the frequencies are converted to probabilities (which range from 0 to 1).  The resulting curve is known as the probability density function or PDF. The sum of the area under the PDF is equal to 1. (Note: Be careful not to confuse capital N, the total number of samples collected, with lower case n, the number of replicates per sample.)

The PDF for a random variable can in theory have almost any shape. In the most general way these can be described as symmetric about the central tendency (i.e., mean), skewed (left or right), or kurtotic (having short tails).  Some specific PDF's of statistical importance that we will discuss include: the Gaussian distribution, Rayleigh distribution, t-distribution, and f-distribution.

Gaussian - This is a symmetric distribution with a single central peak. A subclass of the Gaussian distribution is the normal distribution.

Normal distribution - If the Gaussian distribution has a mean of zero and a standard deviation of 1, it is said to be a normal distribution.  Other names for the normal distribution are the standard distribution or the standard normal distribution.  This is perhaps the most important distribution that we will learn about. The distribution of area under the normal distribution is such that 68% of the observations fall within 1 standard deviation above and below the mean, 95.4% fall within 2 standard deviations and 99.73% fall within 3 standard deviations of the mean. Note that all Normal distributions are Gaussian, but not all Gaussian distributions are Normal! It is, however, possible to transform a Gaussian distribution to a normal distribution by calculating z-scores from the observations in the Gaussian distribution. This is done by subtracting the mean of (x-bar ) from each observation (x_i) in the PDF, and dividing the difference by the standard deviation (σ_x) of x:

z_i = (x_i - x-bar)/σ_x

Z-scores are also refereed to as standard z-scores or standard scores. Table III, the Normal distribution, in Kachigan or other statistical texts, can be used to determine the proportion of the Normal distribution greater than a given z-score.

Rayleigh - The Rayleigh distribution is a distribution that is skewed right.  This is a common distribution in the earth sciences.  Black body radiation from stars, the distribution of grain size in sediment samples and the abundance of marine plankton all exhibit Rayleigh-like distributions.  One interesting property of the Rayleigh distribution is that the log of the Rayleigh distribution is approximately normal in distribution. A log transformed Rayleigh distribution is thus said to be log normal.

t-distribution - is a family of symmetric distributions similar to the normal distribution, but the t-distribution has greater area in its tails.  These distributions arise from averaging small numbers of replicate samples drawn from the population of a random variable.  The shape of the t-distribution approaches that of the normal distribution as the sample size and thus degrees of freedom increases. This distribution is the basis for statistical hypothesis testing of sample population means using the t-test.

f-distribution  -  is a family of right skewed distributions similar to the Raleigh distribution.  These distribution arises from the mean ratio of variance of small numbers of replicate samples drawn from the populations of two random variables.  This distribution is the basis for statistical hypothesis testing of comparison of population variance using the f-test.

The normal distribution is extremely important from a statistical standpoint because we know very precisely the relationship between a particular z-score and the likelihood or probability of its occurrence. That likelihood is simply the area under the normal curve greater than the z-score in question. This will form the basis for quantitative hypothesis testing using the large sample z-test that will be discussed below. What however can be done in situations where we don't know the characteristics of the PDF of a random variable of interest, or worse, if we know that the PDF is non-normal in shape?

In such situations (which are almost all situations!) The Central Limit Theorem provides an empirical solution to the problem.

The Central Limit Theorem as described in Kachigan states:

If a random variable x has a distribution with a mean μ and and standard deviation σ, then the sampling distribution of x, based on replicated random samples of size n, will have a mean, x-bar, equal to the population mean μ, and a standard deviation defined as:

σ_x-bar = σ/√n

The PDF of this random variable will tend toward the normal distribution as the number of replicates per sample n, becomes large.

This is very good news indeed, especially if we can determine how "large", n must be.  As we will see below, this becomes important in terms of hypothesis testing (defined below) because it determines the type of statistical test that is most appropriate to apply. Kachigan suggests that numerous studies find n=30 is sufficiently large. In such situations, use of the large sample z-test for parametric hypothesis testing may be warranted. The alternative statistical test one could use for parametric hypothesis testing would be the small sample t-test (see below).  While n=30 is a fairly conservative estimate, some statisticians might disagree.  Perhaps the best evidence to the contrary is the fact that critical values for the t-distribution are tabulated for degrees of freedom as great as 120! So a more caution approach might be to apply the t-test for n<=120, and the z-test for n>120.

In either case, methods for testing the degree of normality of the distribution should be applied. Use of the z-test for smaller sample may be appropriate due to the character of the PDF of the specific random variable in question. There are at least three methods of doing this:

1. Histogram method - plot the histogram of the data distribution with a superimposed normal distribution to visual check normality.

2. Normal deviates plot - plot tabulated z-scores for the normal distribution against calculated z-scores for the data distribution.  The points should plot along a straight 1:1 line with zero intercept.

3. Chi-Squared goodness-of-fit test - One calculates a statistical called a chi-squared value and compares it against tabulated values to determine if the distribution is normal.  This test is beyond the scope of this course and will not be discussed further.

In the previous section, we used the terms sample size, n, and degrees of freedom when discussing the Central Limit Theorem as if they were identical. This is not strictly the case and warrants further discussion.  The degrees of freedom is a measure of the amount of information used to calculate a statistic about a random variable. Degrees of freedom are related to the number of samples we collected, but become smaller than n for each additional statistic that we calculate from the same data. If we think back to the definition of the mean:

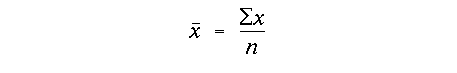
We see that the degrees of freedom of the mean is denoted df = n.  This is true because the central tendency is the simplest statistic that we can calculate. (We know no summary or descriptive statistics about the distribution before we calculate x-bar).

Now compare this with the definition of the unbiased sample variance:

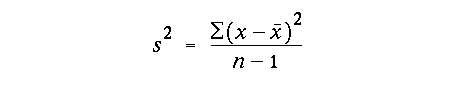
As we pointed out earlier, we normalize this statistic by n-1 degrees of freedom, rather than n, the sample size. Why the difference?  Notice that the variance s² is dependent on the sample mean, x-bar. We thus have only n-1 degrees of freedom left with which to calculate s² because we have used one degree of freedom to calculate the mean. Consider this simple example:  If you knew that the mean (x-bar) of a sample was  3, that n=5 and that the first 4 values were 1, 2, 3, and 4, then you would know from simple algebra that the final value in the sample must be 5.

To generalize the relationship between n and degrees of freedom (df):

where k is the number of statistics already calculated from the same samples. Note however, that this simple estimate of the degrees of freedom provides on upper limit on the true degrees of freedom if the samples extracted from the population are not entirely independent and thus are not truly random. This consideration becomes important in the earth and other natural sciences as many processes tend to produce samples that are influenced by persistence in time or space, i.e. the tendency for a sample x_i collected at time t_i or place z_i to be at least partly dependent on the value x_i-1 obtained at the time t_i-1 or nearby location z_i-1. We will discuss strategies for dealing with this problem in later sections of the notes when we discuss time series analysis. It is important to use the proper degrees of freedom when calculating statistics or reading critical values from tables or the results will be biased and incorrect.

In Statistics, we calculate a test statistic (z-score or t-score) to determine how an observed sample mean (x-bar) relates to a known, true population mean μ, or another sample mean, say x'-bar.  This procedure is known as hypothesis testing.  As described in Devore and Peck, one of the statistical texts listed in the bibliography, the procedure for evaluating a statistical hypothesis includes: (1) developing one null hypothesis, (2) developing one alternative hypothesis, (3) deciding upon a rejection region (p=significance level) which determines the critical value for the test, (4) calculating the test statistic based on the observations, and  (5) comparing the test-statistic with the critical test-value to determine if the null hypothesis can be rejected. The critical value for the test is based on the desired level of significance of the test and the degrees of freedom, if appropriate. It is determined from statistical tables or is calculated based on the properties of the theoretical PDF associated with the statistic. Conducting the procedure in this order is important to prevent the potential for bias. ("Well it's not significant at the level that I picked, maybe I should just change my significance level..."). In practice, computer programs now take input sample data, calculate the desired test statistic based on user input, then report the measured significance level. I cannot stress enough how important it is to understand how the software calculates the test statistic and degrees of freedom. If you select a test or software settings that are not appropriate for your situation, the computer will faithfully provide an incorrect result. Remember the programmers first rule: "Garbage in = garbage out!"

Z-test (large sample mean test)

Suppose you want to know if a measured mean value based on n samples differs from some hypothesized population mean, μ. In cases where the sample size, n, is large and you are absolutely certain that the distribution is Gaussian, then the z-test is the appropriate test to use. The appropriate table for the z-test is the table of z-scores for the normal distribution, Table III in Kachigan. Note that the z-test is not dependent on any degrees of freedom. (Check the Z-Table out - there are no df listed!) The reason for this is that we assume that the distribution is Gaussian, thus the measured standard deviation is assumed to be a true estimate of the population standard deviation and would not depend on th sample size. Use this test with caution if you are not absolutely certain regarding the nature of the distribution or the true degrees of freedom! As a conservative rule of thumb, keep in mind that the t-table is tabulated up to df=120.

A variant of the z-test for a large sample mean is the z-test for the mean difference between non-independent paired samples. In this form of the z-test, we employ pairs of identical samples (for example, a before-after treatment pair). We begin by calculating the mean difference between each pair, decide upon the hypothesized difference, and calculate the standard deviation of the paired difference. We then proceed with the test as described below.

For the z-test:

Null hypothesis

    Ho: μ = some hypothesized value.
    z-test statistic:  z = [x-bar - hypothesized value] / [s/sqrt(n)]

    where s is the standard deviation for x, and n is the number of samples

    The critical z-score is obtained from the Z-table and yields an estimate of p, the significance level.

There are three potential alternative hypotheses:

Upper-tailed test
        Ha : μ > hypothesized value
        Rejection region: reject Ho if z > z-crit

Lower-tailed test
        Ha: μ < hypothesized value
        Rejection region: reject Ho if z < - z-crit

Two-tailed test
        Ha : μ is not equal to the hypothesized value
        Reject Ho if either z > z-crit or if z < - z-crit

How can we test a hypothesis about a mean value when n is small?  The Student's t-test rather than the z-test, is the appropriate way to go when n is small. In practice, the t-test is very similar to the z-test.  The test is based on a comparison of the sample statistics of x with the theoretical values for the t-distribution for the same degrees of freedom. Keep in mind that there is more area in the tails of the t-distribution than the normal distribution. As the number of degrees of freedom increases, the t-distribution converges on the normal distribution. The primary difference between the z-test and t-test is thus that critical values from the t-distribution with appropriate degrees of freedom are used in place of the z-scores from the normal distribution (Table IV from Kachigan).  To use the t-table, you determine the level of significance you wish to test for, find the number of degrees of freedom that are appropriate and then read off the critical value for comparison with the calculated t-statistic.

There are actually several variants of the t-test that are each designed for a particular sampling procedure. We shall see that the primary difference between them is the way in which we quantify the standard deviation of the sampled population or populations. This of course means that some forms of the t-test differ in terms of the degrees of freedom on which they are based.

We will begin with the simplest of the t-test variations, the small sample test for a mean difference. In this application, we are testing to see whether samples in one population differ from some hypothesized value.

For the small sample mean test, all of this can be written as follows:

Null hypothesis

    Ho: μ = some hypothesized value.
    t-test statistic:  t = [xbar - hypothesized value] / [s/sqrt(n)]
                                   for the t-distribution with n-1 df

        where s is the standard deviation for x, and n is the number of samples

There are three potential alternative hypotheses:

Upper-tailed test
        Ha : μ > hypothesized value
        Rejection region: reject Ho if t > t-crit

Lower-tailed test
        Ha: μ < hypothesized value
        Rejection region: reject Ho if t < - t-crit

Two-tailed test
        Ha : μ is not equal to hypothesized value
        Reject Ho if either t > t-crit or if t < - t-crit

Paired Student's t-test (small sample test for a difference between non-independent paired means)

The paired controlled experiment is a particularly powerful design because it provides a means to control for systematic error between control and treatment groups. Consider an example in which you want to evaluate the impact of a fertilizer on plant growth. We could randomly select 12 fields, then randomly subsample that set into two groups, fertilize half of them, and use the other half as a control. There are at least two weakness to this unpaired approach. The first is that by cutting the sample in half we decrease our degrees of freedom by ~2. The second is that there may be some unknown and unmeasured difference between the two groups of fields that will influence the results. Perhaps the fields in one group have poor drainage, are more exposed to wind, or have higher concentrations of plant pests that will limit plant growth? There could be no way to untangle this systematic bias from our results.  Fortunately, there is another approach that we can take. Instead of sorting the fields into groups, we could conduct a before and after fertilizer treatment on all 12 of the fields. The advantage here is that each individual field would be a member of both groups, so that any systematic bias will be minimized while the degrees of freedom in the study are maximized. (We would still potentially need some way to control for temporal differences, but hey, nothing is perfect!) Because all of the samples belong to both groups, the two groups are not independent, and thus hold correlated information. The best way to deal with this is thus to test for the difference in growth between each pair of fields. If the treatment has an effect we would expect that on average we should see a positive increase in the data from the fields following the treatment. Note that the difference between each of the pairs of fields must be calculated in the same way (i.e. x' - x with x' = after) or the potential results will be obscured. This test assumes that the standard deviation of the two sets of samples is the same.

For the small sample test for a difference between non-independent paired means, all of this can be written as follows:

Null hypothesis

    Ho: (μ'-μ) = some hypothesized value for the difference between μ' treated and untreated μ fields
    t-test statistic:  t = [x_d - hypothesized value] / [s_d/sqrt(n)]
                                   for the t-distribution with n-1 df

        where x_d = mean of the x'-x paired differences, 

        and s_d = standard deviation of the x'-x paired differences

        and n = the number of pairs

There are three potential alternative hypotheses:

Upper-tailed test
        Ha : (μ'-μ) > hypothesized value
        Rejection region: reject Ho if t > t-crit

Lower-tailed test
        Ha: (μ'-μ) < hypothesized value
        Rejection region: reject Ho if t < - t-crit

Two-tailed test
        Ha : (μ'-μ) is not equal to hypothesized value
        Reject Ho if either t > t-crit or if t < - t-crit

Two-sample Student's t-test (small sample test for a difference between two independent means)

In many applications in the Earth Sciences, we cannot employ a direct experimental approach because the processes in question operate on timescales that are too short, or too long or on spatial scales that are similarly unmanageable. Alternatively, we may be using data that was collected previously without knowledge of the test that we have in mind. In such a case, it is usually not possible to implement an elegant, paired controlled study. We do have a means at our disposal to deal with this situation. In cases like this, we can't assume that the standard deviation of the two sample groups will be identical. The best approach to dealing with this problem is to calculate a weighted average or pooled standard deviation. Notice also that because we have two populations which may be distinct, the hypothesized value is a difference between two population means.

For the small sample test for a difference between two independent means, all of this can be written as follows:

Null hypothesis
 

    Ho: (μ₁-μ₂) = some hypothesized difference.
    t-test statistic:  t = [(x₁-x₂) - (μ₁-μ₂)] / [sqrt(s_p²/n₁ + s_p²/n₂)]

                                   for the t-distribution with (n₁+ n₂ - 2) df

        where the pooled standard deviation, sp = [(n₁-1)s₁² + (n₂-1)s₂²]/[n₁+n₂-2]

        which is based on the sample standard deviations, s₁ and s₂

                                                        and    n₁ = the number of samples for x₁

                                                        and    n₂ = the number of samples for x₂

There are three potential alternative hypotheses:

Upper-tailed test
        Ha : (μ₁-μ₂) > hypothesized value
        Rejection region: reject Ho if t > t-crit

Lower-tailed test
        Ha: (μ₁-μ₂) < hypothesized value
        Rejection region: reject Ho if t < - t-crit

Two-tailed test
        Ha : (μ₁-μ₂) is not equal to hypothesized value
        Reject Ho if either t > t-crit or if t < - t-crit

There are two type of errors that can be made in hypothesis testing.  A type I error occurs when you reject a null hypothesis that is true.  The probability of this event occurring is equal to alpha, the significance level of the test. A type II error occurs when you fail to reject a null hypothesis that is false. Estimating the probability of encountering a type II error (denoted beta) is more involved than estimating the probability of a type I error.

Beta depends on four factors:

(1) The true difference between the sample estimate and the true value of the
     population parameter. (Beta decreases as the difference between these two increases.)
(2) The significance level alpha used to evaluate the null hypothesis and whether the
     test is one sided or two sided. (Beta increases as alpha decreases.)
(3) The standard error of the sampled population. (Beta increases as sigma increases.)
(4) The size of the sample n. (Beta decreases as n increases.)

Estimating beta is referred to as determining the power of a test. A more detailed discussion of statistical power is beyond the scope of this course, other than to state that perhaps the safest way to avoid type I and type II errors is to increase the sample size, n.