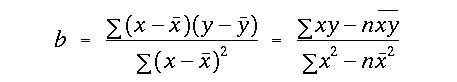
Predictive Methods
Defining the Linear Regression Model
Assumptions of the method
Evaluating the Fit
    A measure of the model error
    How much variance is explained?
    Confidence Interval for the slope, Beta

    Confidence Interval for the regression line
    Confidence Interval for future predictions

With the exception of the mean and standard deviation, linear regression is possibly the most widely used of statistical techniques.  The reason for this is natural.  Many of the problems that we encounter in research settings require that we quantitatively evaluate the relationship between two variables for predictive purposes. By predictive, I mean that the values of one variable depend on the values of a second. We might be interested in calibrating an instrument such as a pump.  We can easily measure the current or voltage that the pump draws, but specifically want to know how much fluid it pumps at a given operating level.  Or perhaps we are interested in determining how the performance of a particular stock relates to a relevant sector index such as the S&P 500.  Or we may want to empirically determine the production rate of a chemical product given specified levels of reactants.

Linear regression, which is the natural extension of correlation analysis, provides an great starting point toward these objectives.

Before we take too detailed a look at the method, let's consider some terminology and see how linear regression relates to other predictive methods.  Because linear regression is such a wide spread method, there is considerable jargon that surrounds the technique.

Terms for predictive analysis:

curve fit - This is perhaps the most general term for describing a predictive relationship
                 between two variables, because the "curve" that describes the two variables
                 is of unspecified form.

polynomial fit - A polynomial fit describes the relationship between two variables as a
                         mathematical series. Thus a first order polynomial fit (a linear regression) is
                         defined as  y = a + bx. A second order (parabolic) fit is y= a + bx + cx^2,
                         a third order (spline) fit is y = a + bx + cx^2 + dx^3, and so on...

Best fit line  - The equation that best describes the y or dependent variable as a function
                      of the x or independent.

linear regression and least squares linear regression - This is the method of interest.  The objective of linear regression analysis is to find the line that minimizes the sum of squared deviations of the dependent variable about the "best fit" line.  Because the method is based on least squares, it is said to be a BLUE method a Best Linear Unbiased Estimator.

Generalized linear regression vs. Regression with zero mean and standardized regression -

Generalized Linear regressions take the form y = a + bx. This type of regression model can used used with data that have none zero mean values.  Regression with zero mean or regression through the origin is a specific case in which a=0. In standardized regression the x and y values are transformed to standardized scores, thus mu(x) = mu(y) = 0, and sigma(x) = sigma(y) = 1. In these cases the best fit line passes through the origin.

Simple linear regression vs. multiple linear regression  -

In simple linear regression, we relate one x  (independent) variable and one y (dependent) variable.  In multiple linear regression, we related two or more independent variables to one dependent variable.  We'll discuss this multivariate method later in class.
 

We've already stated that the general form of the generalized linear regression is:
y= a + bx. The coefficient "a" is a constant called the y-intercept of the regression.
the coefficient "b" is called the "slope" of the regression. It describes the amount of
change in y that corresponds to a given change in x.

The slope of the linear regression can be calculated in a number of ways:

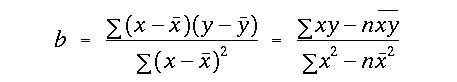
Specifically, the slope is defined as the summed cross product of the deviations of
x and y from their respective means, divided by the sum of squares of the deviations
x from it's mean.  The second relationship above is useful if these quantities have
to be calculated by hand.

It's interesting to note that the slope in the generalized case is equal to the the linear correlation coefficient scaled by the ratio of the standard deviations of y and x:

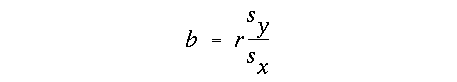
This explicitly defines the relationship between linear correlation analysis and linear regression. Notice that in the case of standardized regression, where sy and sx = 1,
the slope is identical to the correlation coefficient!

The intercept is defined as:

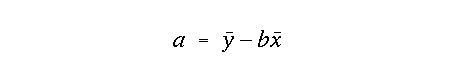
From this definition, it should be clear that the best fit line passes through the mean values for x and y.

There are several assumptions that must be met for the linear regression to be valid:

1. The random variables must both be normally distributed (bivariate normal) and linearly related.

2. The x values (independent variable) must be free of error.

3. The variance of y (the dependent variable) as a function of x must be constant.
This is referred to as homoscedasticity.

A measure of the model error

The scatter of the y values about y estimates (denoted yhat) based on the best fit line is often referred to as the "standard error of the regression":

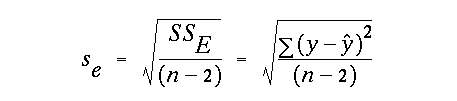
This terminology is confusing because we learned earlier in class that a standard error is defined as the standard deviation divided by the square root of n.  The statistic above actually looks more like the definition of the standard deviation, than a standard error! Notice that two degrees of freedom are lost in the denominator: one for the slope and one for the intercept. A more descriptive definition - and strictly correct name - for this statistic is the root mean square error (denoted rms or rmse). Note: in the book the statistic Se is denoted S y.x

How much variance is explained?

Just as in linear correlation analysis , we can explicitly calculate the variance explained by the regression model:

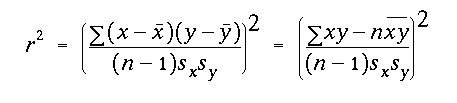
You should recognize this definition as identical to the one used in correlation analysis. This relationship can also be written in terms of the z-scores of x and y.  Make sure that you understand how that can be done.

Determining statistical significance

As with the other statistics that we have studied the slope and intercept are sample statistics based on data that includes some random error, e:

We are of course actually interested in the true population parameters which are defined without error.

Be careful not to confuse these alpha's and beta's with the alpha's and beta's that relate to the significance levels of the type 1 and type 2 errors discussed in hypothesis testing. They are not the same things! Unfortunately sometimes in statistics there are too few Greek letters to go around.

How do we assess the significance level of the model? In essence we want to test the null hypothesis that b=0 against one of three possible alternative hypotheses:

There are at least two was to determine the significance level of the linear model. Perhaps the easiest method is to calculate r, and then determine significance based on the value of r and the degrees of freedom using a table for significance of the linear or product moment correlation coefficient. This method is particularly useful in the standardized regression case when b=r.  What can be done, however, in the general case when b=r(sy/sx)? Fortunately, there is a better way to evaluate the generalized linear regression.

We can determine the significance level of b, by calculating a confidence interval for the slope. Just as we did in earlier hypothesis testing examples, we determine a critical t-value based on the correct number of degrees of freedom and the desired level of significance. It is for this reason that the random variables x and y must be bivariate normal. For the linear regression model the appropriate degrees of freedom is always df=n-2. The level of significance of the regression model is determined by the user, the 95% or 99% levels are generally used.  The confidence interval is then defined as the product of the critical t-value and S_b, the standard error of the slope:

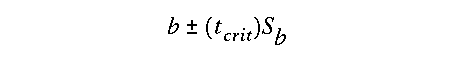
where S_b is defined as:

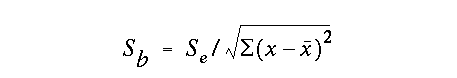
Interpretation of this result is easy.  If there is a significant slope, then b will be statistically different from zero.  So if b is greater than (t-crit)*S_b, the confidence interval does not include zero. We would thus reject the null hypothesis that b=0 at the pre-determined significance level.  As (t-crit)*S_b becomes smaller, the greater our certainty in beta, and the more accurate the prediction of the model.

If we plot the confidence interval on the slope, we will see that the positive and negative limits of the confidence interval of the slope plot as lines that intersect at the point defined by the mean x,y pair for the data set. In effect, this tends to underestimate the error associated with the regression equation because it neglects the role of the intercept in controlling the position of the line in the cartesian plane defined by the data. Fortunately, we can take this into account by calculating a confidence interval on line.

Confidence Interval for the regression line

Just as we did in the case for the confidence interval on the slope, we can write this out explicitly as a confidence interval for the regression line, that is defined as follows:

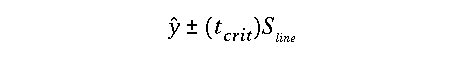
The degrees of freedom is still df= n-2, but now the standard error of the regression line is defined as:

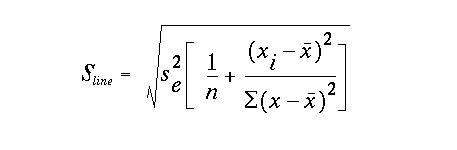
Because values that are further from the mean of x and y have less probability and thus greater uncertainty, this confidence interval is narrowest near the location of the joint x and y mean (the centroid or center of the data distribution), and flares out at points further from centroid. While the confidence interval is curvilinear, the model is in fact linear. You can think of the flaring ends as encompassing all possible slopes and their associated intercepts within the errors of the data.

Confidence Interval for future predictions

It is tempting to think that the rmse can be used to provide a confidence interval on future predictions of y based on measured values of x. In fact, the rmse is often used in this manner.  Such a procedure however, is not strictly correct, because the uncertainty in future predictions of y is a function of three sources of error: (1) the rmse which is effectively a measure of the uncertainty in the y predictions relative to the regression line, (2) the uncertainty in the sample estimate of the y intercept (a), and (3) the uncertainty in the sample estimate of the slope b, which controls the uncertainty in the intercept.  As n increases, the uncertainty in the last two terms decreases, and the uncertainty in the true predictions converges on the rmse.

Just as we did in the case for the confidence interval on the slope, we can write this out explicitly as a confidence interval on the future predictions, yhat that is defined as follows:

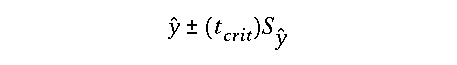
The degrees of freedom is still df= n-2, but now the standard error of the y predictions is defined as:

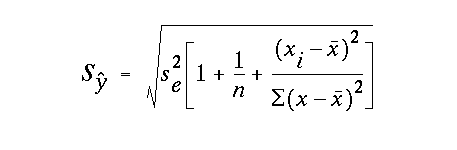
This is the broadest of the three confidence intervalues that we have considered. Notice that 1+(1/n) is equal to (n+1)/n.  This confidence interval is still slightly curvilinear. but because this confidence interval is scaled by (n+1)/n, rather than 1/n, as was the case for the confidence interval of the line, there is considerably less curvature to it.