![]()
Aggregate Method
![]()
![]()
![]()
Application 1: Stack operations
In the following pseudocode, the operation
STACK-EMPTY returns TRUE if there are no object currently on the stack,
and FALSE otherwise.
MULTIPOP(s, k)
while (.NOT. STACK-EMPTY(s) and k
≠ 0)
do pop(s)
k = k-1
Analysis
Application 2: Binary Counter
We use an array A[0 . . k-1] of bits, where
length
[A] = k, as the counter. A binary number x that
is stored
in the counter has its lowest-order bit in A[0] and its
highest-order
bit is A[k-1], so that k-1Si=0
2iA[i].
Initially, x = 0, and thus A[i] = 0 for i=0,
1, . . . ,
k-1.
To add 1 (modulus 2k ) to the value in the counter,
use the following pseudocode.
INCREMENT (A)
i = 0
while i < length [A] and A[i] = 1
do A[i] = 0
i = i+1
if i < length [A]
then A[i] = 1
A single execution of INCREMENT takes O(k)
in worst case when Array A contains all 1's. Thus, a
sequence of n INCREMENT operation on an initially zero counter
takes O(nk) in the worst case. This bound is correct but not tight.
Amortized Analysis
We can tighten the analysis to get a worst-case cost for a sequence of an INCREMENT's by observing that not all bits flip each time INCREMENT is called.
Bit A[0] is changed ceiling n times (every time)
Bit A[0] is changed ceiling [n/21] times (every other time)
Bit A[0] is changed ceiling [n/22] times (every other time)
.
.
.
Bit A[0] is changed ceiling [n/2i] times.
In general, for i = 0, 1, . . .,  lg n
lg n , bit A[i]
flips
, bit A[i]
flips  n/2i
n/2i times in a sequence of
n
INCREMENT operations on an initially zero counter.
times in a sequence of
n
INCREMENT operations on an initially zero counter.
For i > 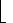 lg(n)
lg(n)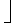 , bit A
, bit A  i
i never flips at all. The total number of flips in a sequence
is thus
never flips at all. The total number of flips in a sequence
is thus
floor(log)Si=0  n/2i
n/2i < n ∞Si=0
1/2i = 2n
< n ∞Si=0
1/2i = 2n
Therefore, the worst-case time for a sequence of n INCREMENT operation on an initially zero counter is therefore O(n), so the amortized cost of each operation is O(n)/n = O(1).
![]()