Bridge    A bridge is a single edge whose removal disconnects a graph.

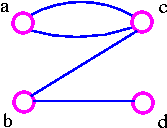
The above graph G1 can be split up into two components by removing one of the edges bc or bd. Therefore, edge bc or bd is a bridge.

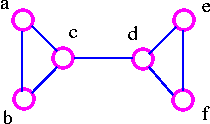
The above graph G2 can be disconnected by removing a single edge, cd. Therefore, edge cd is a bridge.

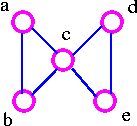
The above graph G3 cannot be disconnected by removing a single edge, but the removal of two edges (such as ac and bc) disconnects it.

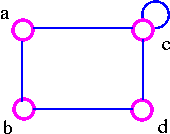
The above graph G4 can be disconnected by removing two edges such as ac and dc.

Edge Connectivity

The edge-connectivity λ(G) of a connected graph G is the smallest number of edges whose removal disconnects G. When λ(G) ≥ k, the graph G is said to be k-edge-connected.

For example, the edge connectivity of the above four graphs G1, G2, G3, and G4 are as follows:

• G1 has edge-connectivity 1.
• G2 has edge connectivity 1.
• G3 has edge connectivity 2.
• G4 has edge connectivity 2.

Cut Set

A cut set of a connected graph G is a set S of edges with the following properties

• The removal of all edges in S disconnects G.
• The removal of some (but not all) of edges in S does not disconnects G.

As an example consider the following graph

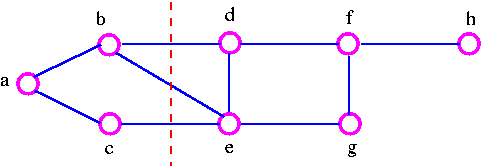
We can disconnect G by removing the three edges bd, bc, and ce, but we cannot disconnect it by removing just two of these edges. Note that a cut set is a set of edges in which no edge is redundant.

Vertex Connectivity

The connectivity (or vertex connectivity) K(G) of a connected graph G (other than a complete graph) is the minimum number of vertices whose removal disconnects G. When K(G) ≥ k, the graph is said to be k-connected (or k-vertex connected). When we remove a vertex, we must also remove the edges incident to it. As an example consider following graphs.

The above graph G can be disconnected by removal of single vertex (either b or c). The G has connectivity 1.

The above graph G can be disconnected by removal of single vertex (either c or d). The vertex c or d is a cut-vertex. The G has connectivity 1.

g46.gif

The above G can be disconnected by removing just one vertex i.e., vertex c. The vertex c is the cut-vertex. The G has connectivity 1.

The above G cannot be disconnected by removing a single vertex, but the removal of two non-adjacent vertices (such as b and c) disconnects it. The G has connectivity 2.

Cut-Vertex

A cut-vertex is a single vertex whose removal disconnects a graph.

It is important to note that the above definition breaks down if G is a complete graph, since we cannot then disconnects G by removing vertices. Therefore, we make the following definition.

Connectivity of Complete Graph

The connectivity k(k_n) of the complete graph k_n is n-1. When n-1 ≥ k, the graph k_n is said to be k-connected.

Vertex-Cut set

A vertex-cut set of a connected graph G is a set S of vertices with the following properties.

1. the removal of all the vertices in S disconnects G.
2. the removal of some (but not all) of vertices in S does not disconnects G.

Consider the following graph

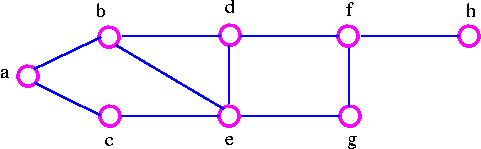
We can disconnects the graph by removing the two vertices b and e, but we cannot disconnect it by removing just one of these vertices. the vertex-cutset of G is {b, e}.

Note that the connectivity k(G) does not exceed the edge-connectivity λ(G). This inequality holds for all connected graph.

Formally, for any connected graph G we have

K(G) ≤ λ(G) ≤ δ(G)

where δ(G) is the smallest vertex-degree in G. But it is certainly possible for both inequality in above theorem to be strict inequalities (that is, k(G) < λ(G) < δ(G)) For example, in the following graph,

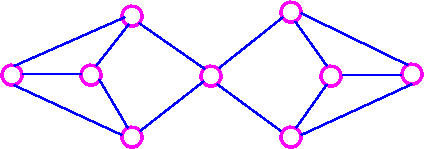
K(G)=1, λ(G) = 2, and δ(G) = 3.

Meneger's Theorem for graph

Edge Form