In this section we introduce the best known parameter involving nonplanar graphs. On a sphere we placed a number of handles or equivalently, inserted a number of holes, so that we can draw a graph with edge-crossings. The number of handles (or holes) is referred to as the genus of the surface and denoted as of or g(G) or gen(G). By the genus, g, of a graph G is meant the smallest genus of all surfaces on which G can be embedded. Every graph has a genus; in fact a graph of size m can be embedded on a surface of genus m.

Since the embedding of graphs on spheres and places is equivalent (we can puncture the sphere and get plane), the graphs of genus 0 are precisely the planar graphs. The graph with genus 1 are therefore the nonplanar graphs that are embeddable on the torus. The (nonplanar) graphs K₅ and K_3,3 have genus 1. Embeddings of K_3,3 and K₅ on the torus are shown below.

Diagram

Genus of a Graph

The term "planar" comprises two conditions.

A graph is planar if

• It is drawn without edge-crossings
• It is drawn in a plane.

The concept "genus" includes the first condition but generalizes the seconds by considering other surfaces.

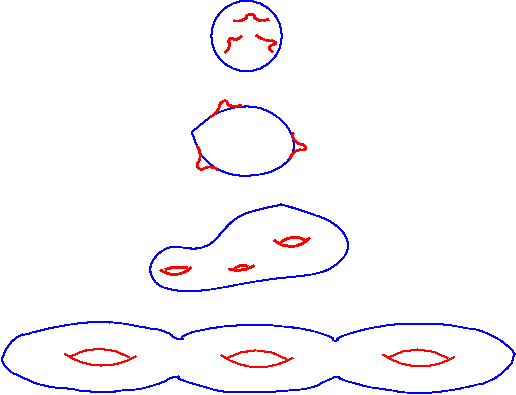
The first four members of an infinite family of surfaces i.e., sphere, one-hole torus, two-hole torus, and three-hole torus are shown below

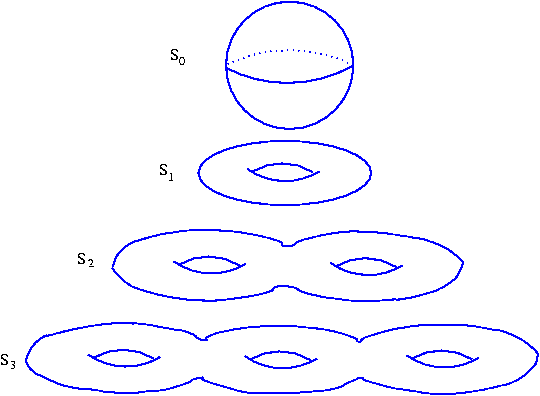
These surfaces are taken to be hollow and of negligible thickness. For example, we should think of S₀ as a beachball rather than a baseball and of S₁ as a valueless inner-tube rather than a doughnut. In the names of the surfaces subscripts refer to the number of holes. Thus, S₀ is a "torus" with no holes,  S₁ is a one-hole torus,  S₁₀₀ is a hundred-hole torus, etc.

Definition

The genus of a graph, denoted "g" is the subscript on the first surface among the family of surfaces,  S₀,  S₁, . . . on which the graph can be drawn without edge-crossings. In this definition we implicitly assumes that every graph has a geuns; That is, given any complicated nonplanar graph G, we can systematically search a sequence S₀, S₁, S₂, . . . that reveal some surfaces on which G can be drawn without edge-crossing. The genus, g, is just the subscript of the first surface.

Theorem 1     The set of all planar graphs is equal to the set of all graphs with g=0.

Proof Idea     Here we have two statements to establish. First, "Every planar graph has g=o" and second "Every graph with g=0 is planar." To prove that two sets are equal we have to show that each is a subset of the other.

This theorem shows that the "planar" concept is merely a special case of the "genus" concept. Planar graphs are the graphs of genus 0.

Note that despite of the fact that edges can go "around the back" of a sphere, we cannot avoid edge-crossings on spheres when they cannot be avoided in a plane.

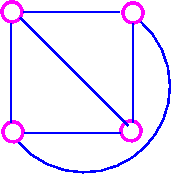
Example1. K₄ has g = 0 because it is a planar.

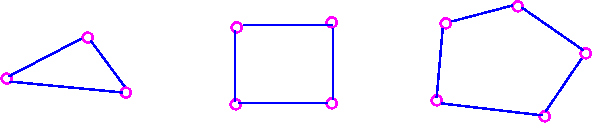
Example 2. Each cyclic graph, C_v, has g=0 because it is planar.

Example 3. The complete bipartite graph K_3,3 (utility graph) has g=1 because it is nonplanar and so by theorem 1 cannot be drawn without edge-crossings on S₀;

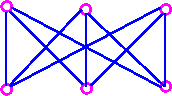
but it can be drawn without edge-crossings on S₁ (one-hole torus or doughnut).

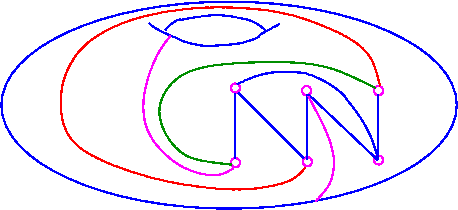
Thus, the subscript 1 in the is S₁ the first surface (doughnut) in the family  S₀,  S₁, . . . on which k_3,3 can be drawn without edge-crossings.

Similarly, K₅ has g=1 for the same reasons see the following figure.

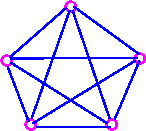
Theorem 2     Every graph has a genus.

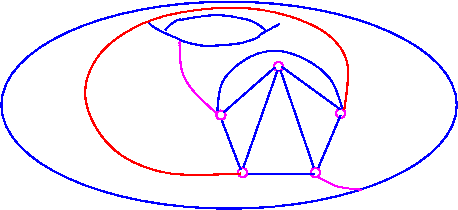
Proof     Let G be any graph. If G is planar it has g=0 by Theorem 1, so let us assume that G is nonplanar. Take a drawing of G in a plane and transfer to the surface of S₀. Add to S₀ enough "handle" to serve as "overpass", thereby eliminating the edge-crossings. This has been shown in the following figure for K₆.

K₆ on Surface S₀

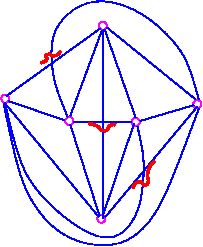
K₆ on Surface S₀ with three handles (or holes).

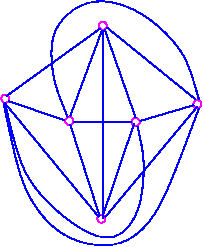
Let the number of handles be n. The number n is finite, as a graph can have only finite number of edges and hence only a finite number of edge-crossings. Topologically, the surface consisting S₀ of with n handles can be "continuously deformed" into S_n and the edges and vertices of G can be carried along with this continuous deformation. Following figure shows this for S₀ with three handles (k₆ have been omitted).

Thus G can be drawn on S_n without edge-crossings. Since there is at least one member, S_n, of the sequence of surfaces S₀, S₁, S₂ on which G can be drawn without edge-crossings, there must be a first such number S_g. Then by definition g is the genus of G and we have the theorem.

Theorem 3     If a graph G has genus g then G can be drawn without edge-crossings on every surface S_n for which n≥g.

For specific graph G, its genus g cuts the sequence S₀, S₁, . . .  into two pieces. The first part S₀, S₁, . . . S_g-1 is finite and consists of all surfaces in the family on which G cannot be drawn without edge-crossings. The second part S_g, S_g+1, . . .  is infinite and consists of all surfaces on which G can be drawn without edge-crossings.

The "genus" is use to specify the extent to which nonplanar graph is "nonplanar". For example a graph of genus 100 is much farther from planarity than a graph of genus 4.

Up to now the term "face" has been defined only for planar graphs (see Planar Graphs). To speak of the "faces" of say, complete bipartite graph, would have been to speak nonsense. But with new family of surfaces it is now possible to define the term "face" for any graph as follows:

If a graph G of genus g has been drawn on the surface of S_g without edge-crossings, then the edges and vertices of G divide the surface of S_g into regions faces of G.

Example k_3,3 has f=3.

<fig 5 --> Edit --> Include faces>

<fig 6 --> Include faces >

Now that "face" makes sense for nonplanar graphs as well, we revisit the Euler formula.

Euler's Second Formula

For every connected graph of genus g,

v + f - e = 2 - 2g

It is easy to see that for planar graphs this reduces to the

v + f - e = 2

Our proof of the Euler's second formula is based on the following assumption that we shall not prove.

Assumption

If G is a connected graph of genus g then there exists a crossing-free drawing of G on S_g such that through each of the g holes of S_g  there is a ring composed of vertices and edges of G.

Here are some examples that make us feel that the assumption is at reasonable.

Example 1

Consider a drawing of k₅ on S₁.

fig 133 (a) pp. 149

The walk BCDB goes around through the hole and back again.

To make a perfect ring out of walk BCDB, the vertices and edges have been rearranged

< fig 133(b) >

Example Consider the drawing of k_3,3 on S₁. Again we have walk, XAYBX, that goes around through the hole.

< fig 134-a >

And again, to make a perfect ring, the vertices and edges have been arranged.

< fig. 134-b >

Our assumption is that a similar phenomenon occurs for any connected graph.

This assumption is reasonable. If G has genus g then G cannot be drawn without edge-crossings on any surfaces having fewer then g holes, so each of the g holes is crucial to waking a crossing-free drawing of G. Therefore, at least one edge of G n=must pass through each hole.

Euler's Second Formula

If G is connected then n - m + f = 2 - 2g.

Proof

Some Consequences of Euler's Second Formula

Lemma 21. If a connected graph G has n≥3 and genus g then

g ≥ (1/6)e - (1/2)(n-2)

Proof

By the lemma we have 3f ≤ 2n. Since G is connected Euler's second formula applies and we have

n - m + f = 2 - 2g.

Rewritten f = -n + m + 2 -2g

multiply by 3

3f = -3n + 3m + 6 -6g

Combining with the inequality, 3f ≤ 2n.

-3n + 3m + 6 - 6g ≤ 2n

which can be rewritten as

-6g ≤ -m + 3n - 6

multiply by -1/6 given

g  ≥ (1/6)m -(1/2)(n-2)

Using the theorem

We can find a lower bound for the genus of a connected graph, even if we know nothing more than its cardinality of vertices and edges. For example, consider the graph with 52 vertices and 201 edges. Then by the theorem we have

g  ≥ (1/6)201 -(1/2)50 = 81/2.

But g is an integer so we can conclude that the genus of G is at least 9.

The next theorem can be used to find an upper bound for the genus of a graph.

Lemma 22. If a graph H of genus g_H can be drawn on S_n without edge-crossing, then g_H≤n.

Lemma 22c. If H is a subgraph of G, then g_H≥g_g.

Theorem 22. If n≥3 the complete graph k_n has genus

g = left ceiling {(n-3)(n-4)}/12} right ceiling.

Corollary 22. If G has n≥3 and genus g then

g ≤ left ceiling {(n-3)(n-4)}/12} right ceiling.

The lower and upper bounds for the genus of connected graph, even if we know only its number of vertices, m, and number of edges, n, is as follows

left ceiling (1/6)e - (1/2)(v-2) right ceiling ≤ g ≤ left ceiling{(v-3)(v-4)}/12 right ceiling.

Conclusion

Euler formula

n - m + f = 2 - 2g

If G is a connected graph with n≥3 then

g ≥ (1/6)m - (1/2)n+1

If G is a connected graph with smallest cycle of length k, then

g ≥ m/2(1 - (2/k)) - (n/2)     1

If G is a connected, triangle-free graph with n≥3, then

g ≥ (1/4)m - (1/2)n+1

If G is a graph having blocks B₁, B₂, . . . , B_k

then

g = ^kΣ_i=1 g(B_i)

A consequence of this result is: If G is a graph with component G1, G2, . . .Gk, then

g = ^kΣ_i=1 g(Gi)

Computing the genus of Graphs

The genus of the complete graph is given by

g(k_n) = left ceiling {(n-3)(n-4)}/12 right ceiling, n ≥ 3.

The genus of the complete bipartite graph is given by

g(k_r,s) = left ceiling {(r-2)(s-2)/4}right ceiling, r,s ≥ 2.

The genus of the n-cube is given by

G(Q_n) = (n-4). 2^n-3 + 1, n≥ 2