An acyclic graph (also known as a forest) is a graph with no cycles. A tree is a connected acyclic graph. Thus each component of a forest is tree, and any tree is a connected forest.

Theorem    The following are equivalent in a graph G with n vertices.

1. G is a tree.
2. There is a unique path between every pair of vertices in G.
3. G is connected, and every edge in G is a bridge.
4. G is connected, and it has (n - 1) edges.
5. G is acyclic, and it has (n - 1) edges.
6. G is acyclic, and whenever any two arbitrary nonadjacent vertices in G are joined by and edge, the resulting enlarged graph G' has a unique cycle.
7. G is connected, and whenever any two arbitrary nonadjacent vertices in G are joined by an edge, the resulting enlarged graph has a unique cycle.

Generally speaking, algorithms associated with trees can be divided into three types.

• Algorithms for searching and labeling a given tree.
• Algorithms for constructing various types of tree.
• Algorithms for counting trees of a particular type.

Tree    A tree is a connected graph which contain no cycles.

For example,

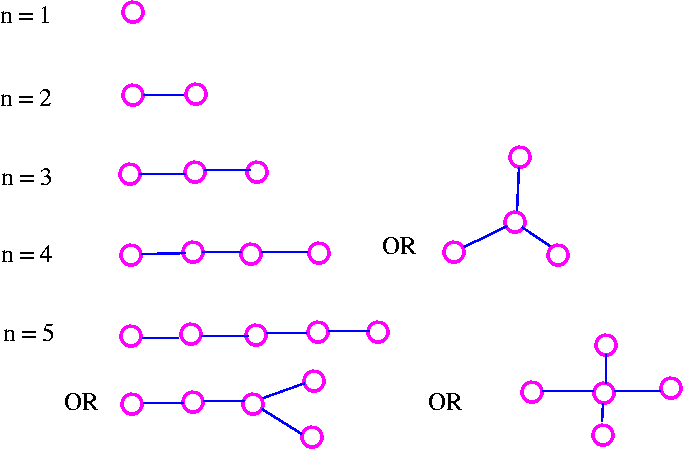
Theorem    Let T be a graph with n vertices. Then the following statements are equivalent.

1. T is connected and contains no cycles.
2. T is connected and has n-1 edges.
3. T has n-1 edges and contains no cycles.
4. T is connected and each edge is abridge.
5. Any two vertices of T are connected by exactly one path.
6. T contains no cycles, but the addition of any new edge creates exactly one cycles.

Spanning Trees

Let G be a connected graph. A spanning tree in G is a subgraph of G that includes all the vertices of G and is also a tree. The edges of the trees are called branches.

For example, consider the following graph G

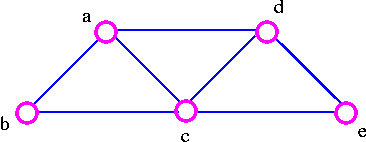
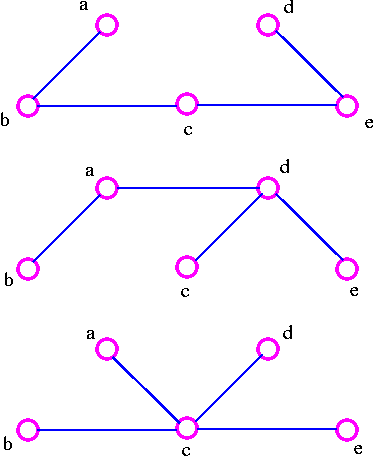
The three spanning trees G are:

We can find a spanning tree systematically by using either of two methods.

• Cutting-down Method
  • Start choosing any cycle in G.
  • Remove one of cycle's edges.
  • Repeat this procedure until there are no cycle left.

                For example, given the graph G

                1. We remove the edge ac which destroy the cycle adca in the above graph and we get

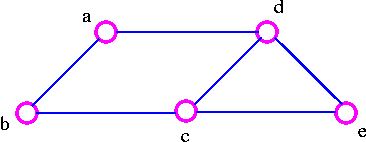
                2. We remove the edge cb, which destroy the cycle adcba in the above graph and we get

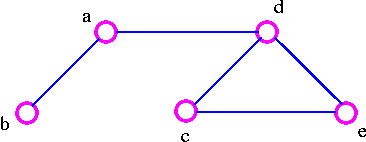
                3. We remove the edge ec, which destroy the cycle decd in the above graph and thus obtained the following spanning tree.

• Building-up Method
  • Select edges of G one at a time. in such a way that no cycles are created.
  • Repeat this procedure until all vertices are included.

                For example, for the following  graph G

                1. Choose the edge ab

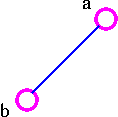
                2. Next choose the edge de as follows:

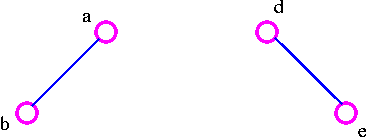
                3. After that choose the edge ec as follows:

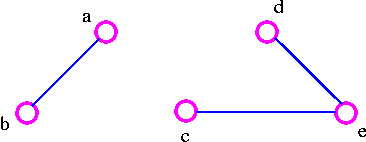
                4. Finally, we choose the edge cb and thus obtain the following spanning tree.

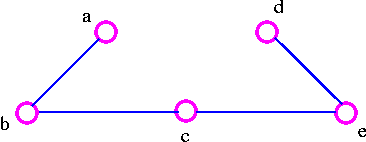
Theorem     A graph is connected if and only if it has a spanning tree.

Proof    Let G be a connected graph. Delete edges from G that are not bridges until we get a connected subgraph H in which each edge is a bridge. Then H is a spanning tree. On the other hand, if there is a spanning tree in G, there is a path between any pair of vertices in G; thus G is connected.

Centers and Bicenters

It is convenient to start building up the tree at the middle of a tree and move outwards. This was the approach used by Arthur Cayley when he counted the number of chemical molecules by building them step by step. But what do we mean by the "middle" of a tree?

There are two straight forward ways to compute centers and bicenters.

Algorithm1

• Remove all the vertices of degree1, together with their incident edges.
• Repeat the process until we obtain either a single vertex (the center) or two vertices joined by an edge (the bicenter).

A tree with a center is called a central tree, and a tree with a bicenter is called a bicentral tree. Note that every tree is either central or bicentral, but not both.

For example, given a following tree.

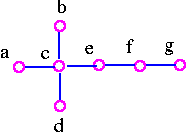
Remove all vertices of degree 1.

Remove all vertices of degree 1.

Therefore, a tree is central with center e.

Another example, given a following tree.

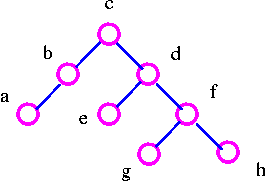
Remove all vertices of degree 1.

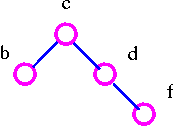
Remove all vertices of degree 1.

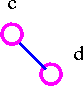
Therefore, a given tree is bicentral with bicenter cd.

Algorithm 2

For each vertex v of the degree 2 or more, count the number of vertices in each of the subtrees emanating from v, and let n_v be the maximum of these numbers. If the tree has n vertices it can be shown that either there is just one vertex v for which n_v ≤ 1/2(n-1) (the centroid or centroid tree) or there are two adjacent vertices v and w for which n_v = n_w = 1/2n (the bicentroid or bicentroid tree). It is easy to see that every tree is either centroidal or bicentroidal, but not both.

Note that we can think of the centroid or bicentroid as the 'center of gravity' of the tree.

For example, given a following tree

Since n_c = 4, n_e = 4, n_f = 5 and n_g = 6. Therefore, we have a bicentroidal tree with bicentroid ce.

Another example, given a following tree.

Since n_b = 6, n_c = 5, n_d = 3 and n_f = 5. Therefore,  we have a centroidal tree with centroid d.

Tree Searching

There are two well-known search methods. They are brown as depth-first search( DFS) and breadth-first search (BFS). Each of these methods lists the vertices as they are encountered, and indicates the direction in which each edge is first traversed. The methods differ only in the way in which the vertex-lists are constructed.

Depth-First Search (DFS)

The basic idea of depth-first search is to penetrate as deeply as possible into a tree before fanning out to other vertices. This idea may be depicted as follows:

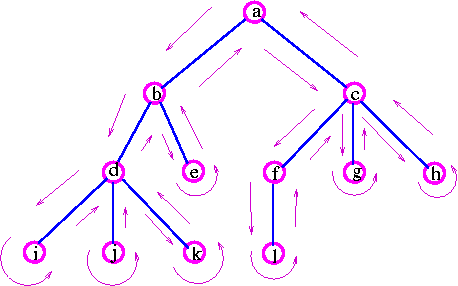
a -> b --> d --> i -> j -> k -> e -> c -> f -> i -> g  -> h.

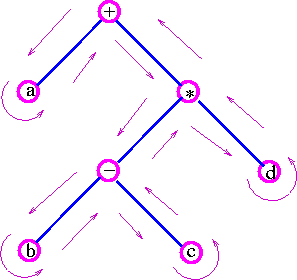
Another example, the expression a + {(b-c) × d} can represented by following tree:

Example: Consider the graph

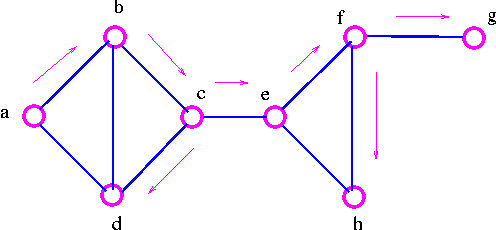
Note that we have marked those edges we used when going to new vertex. These edges form a spanning tree, called a DFS spanning tree.

Breadth-First Search (BFS)

The basic idea of breadth-first search is to fan out to as many vertices as possible before penetrating deep into a tree. This idea may be depicted as follows:

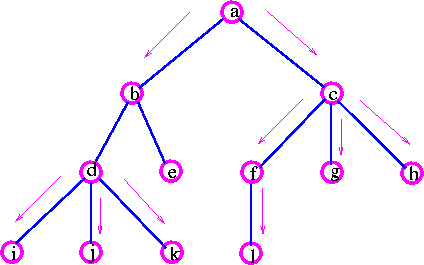
a --> b --> c --> d --> e --> f --> g --> h --> i --> j --> k --> e

above example clearly shows that breadth-first search must complete each level before proceeding to the next one.

Example: Consider the graph

Note that we have marked those edges we used when going to new vertex. These edges form a spanning tree, called a BFS spanning tree.