First Part (10 point questions

Other things equal, when demand increases, the price rises and supply increases. Explain whether you disagree or disagree with this statement. Disagree. The quantity supplied will increase, but there is simply a movement along the supply curve.
As you know, March 7 is primary day in Ohio. The campaign between John McCain and George W. Bush will to be fierce. A prominent political scientist has concluded that

George W. Bush’s view is that a win is a win is a win. The margin does not matter.
John McCain’s view is that the size of the win or loss matters. He would rather win by many votes than few votes (and similarly would rather lose by few votes than by many votes)

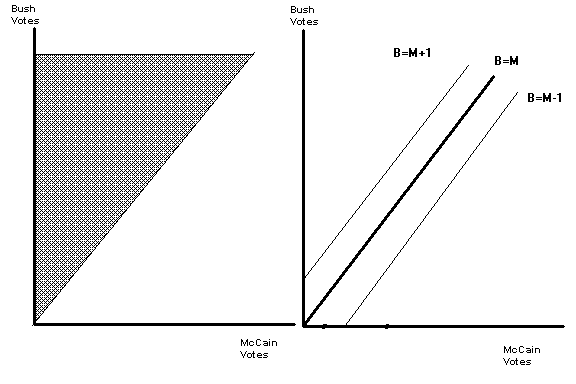
Take the political scientist at his word. Draw indifference curves for John McCain and George Bush for the number of votes each gets. Label your axes clearly. Defend your answers. WARNING. These indifference curves are not exactly standard. Don’t draw them blindly. Think through the problem.

The following graph illustrates the two cases. The first panel illustrates Bush’s preferences; the second panel, McCain’s. To illustrate Bush’s preferences, I have drawn a 45-degree line. Bush wants to be above that line. Any point above that line is preferable to any point below that line. The indifference curves are not standard. John McCain’s preferences are more perhaps more standard. I have drawn three indifference curves. One, the 45 degree line going through the origin is labeled B = M, corresponding to Bush and McCain getting an equal number of votes. This corresponds to a tie and is certainly an indifference curve. The line B=M+1 corresponds to Bush beating McCain by one vote and lower level of utility for McCain. The line B=M-1 corresponds to a one vote McCain victory and, of the three indifference curves drawn the highest level of utility for Senator McCain. You can draw other indifference curves but these three give the general picture.

April Summer is a risk taker. That means the higher the level of income, the more utility she would lose from a $1,000 loss. Explain whether you agree or disagree. Agree. The concept of risk taker is one for whom the marginal utility of income rises with income. That is exactly what this statement says.
John Wilton, PhD, purchases 10 kumquats a week from Acme Fruit and vegetable. Acme charges $1 each. He loves Kumquats. A new fruit stand, Everfresh Fruits, opens next door. Everfresh sells Kumquats at $1.25 each, but they have a standard weekly special on kumquats at 75 cents, with a maximum of five to a customer. John, clever lad that he is, quickly sees through this bait and switch advertising will ignore Everfresh and continue to purchase 10 kumquats a week from Acme. Explain whether you agree or disagree.. Disagree. John will switch to Everfresh and purchase fewer than 10 kumquats a week. He can thereby move to a higher indifference curve.

Second Part (30 point questions)

Directions: Work any two (2) of the following three (3) questions. In the boxes below, check which problems you have worked: If you do not check the boxes, I will assume you want to work problems 1 and 2.

*I have worked(Check 2)*
*Problem 1*
*Problem 2*
*Problem 3*

1. The demand functions for two products A and B are:

P_A = 40 - (0.05)Q_A

Q_B = 800 - 20P_B

For each demand function,

(a) compute the point price elasticity (h) at P = 20.

These are really the same demand functions, as you can see by reversing the first equation and putting Q_A on the left-hand side. When P = 20, Q = 400, and Delta Q/Delta P = -20. Thus the elasticity is given by

h = (P/Q)(Delta Q/Delta P ) = (20/400)(-20) = -1

(b) compute the arc price elasticity when the price changes from P =15 to P = 25.

The average value of P is 20. The Average value of Q = 400. Delta Q/Delta P is unchanged. Thus the arc price elasticity is

h = (P/Q)(Delta Q/Delta P ) = (20/400)(-20) = -1

2. The demand per household for a product is given by q = 12-3p.

· Compute consumer surplus assuming that the product is given away freely.

· Compute consumer surplus assuming that the product is sold at a price of $1 per unit.

· Now suppose the government imposes a tax of $1 on each unit of the product that is consumed. The proceeds of the tax are distributed to individuals in the community, independent of how much of the product they consume. What is the deadweight loss?

The triangle has a base of 12 and a height of 4. Thus the consumer surplus is (1/2)(12)(4) = 24. If the product is sold at $1 each, demand is 9, and the consumer surplus is (1/2)(9)(3) = $13.50. When the government imposes the tax, the demand drops to 6. The deadweight loss is (1/2)(1)(3) = $1.50. Remember that the deadweight loss applies only to the products no longer consumed.

3. Use the data in the following table to answer the question.

K = 10		K=20		K=30
Q	TC($)	Q	TC($)	Q	TC($)
0	50	0	100	0	150
2	80	2	120	2	160
4	120	4	150	4	180
6	180	6	190	6	210
8	320	8	240	8	250
10	500	10	340	10	320
12	750	12	550	12	400

The firm also knows that it is a price-taker at $35 per unit. (Obviously K – unites of capital, Q is quantity produced and TC is total cost).

1. What constitutes this firm’s long run profit maximizing level of output?

2. If the firm is operating at its long run profit maximizing level of output, what action would it undertake in the short run if the price rose to $45 a unit?

3. What action would the firm undertake in the long run if the price rose to $50 a unit.

4. Explain why your answers to 2 and 3 are the same, if they are, or why they are different, if they are.

Answer

Let me answer the questions in order. The long run cost function is given by the points in the following table. I have added a fourth column giving the long run marginal cost of going from 0 to 2 to 4 units, etc. Each two units sells for $70, and it is clear that marginal cost is still below price at Q = 8. Going from 8 to 10 units of output would cost the firm money.

Q	TC	K	MC
0	$50	10	NA
2	$80	10	$30
4	$120	10	$40
6	$180	10	$60
8	$240	20	$60
10	$320	30	$80
12	$400	40	$80

In the short run where it was stuck with a value of K = 20, it would increase output to 10 units. In the long run, it would change K to 30 and increase output further to 12 units. The difference between the answers to 3 and 4 comes about because of the inability to change K in the short run