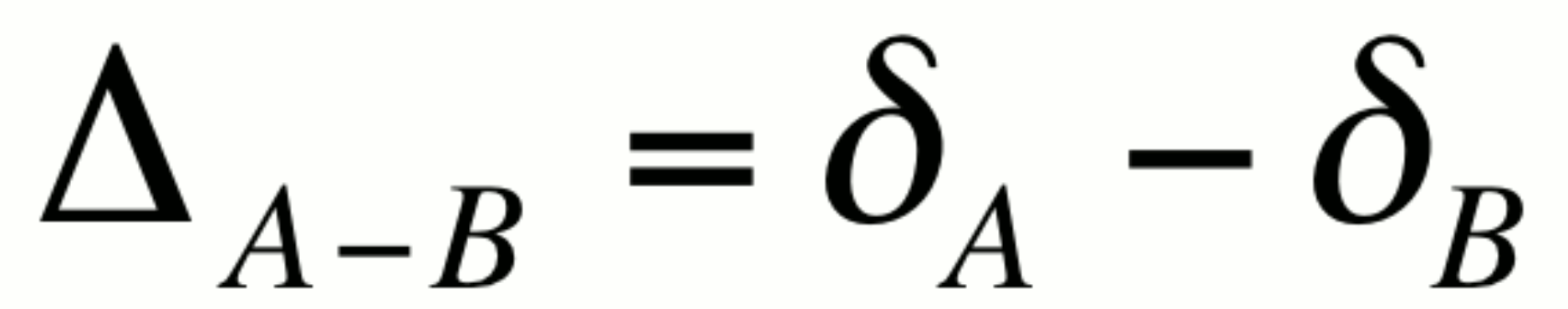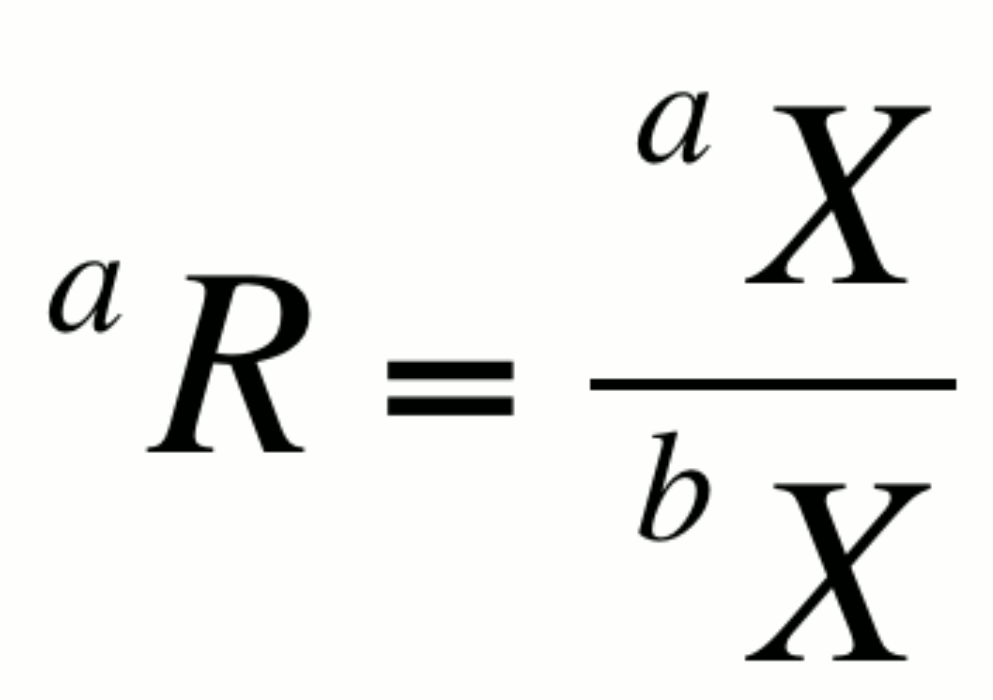
A Primer on Isotope Notation

 

The isotope ratio:

The relative abundance of two isotopes a and b of element X can be expressed as an isotopic ratio, ^aR:

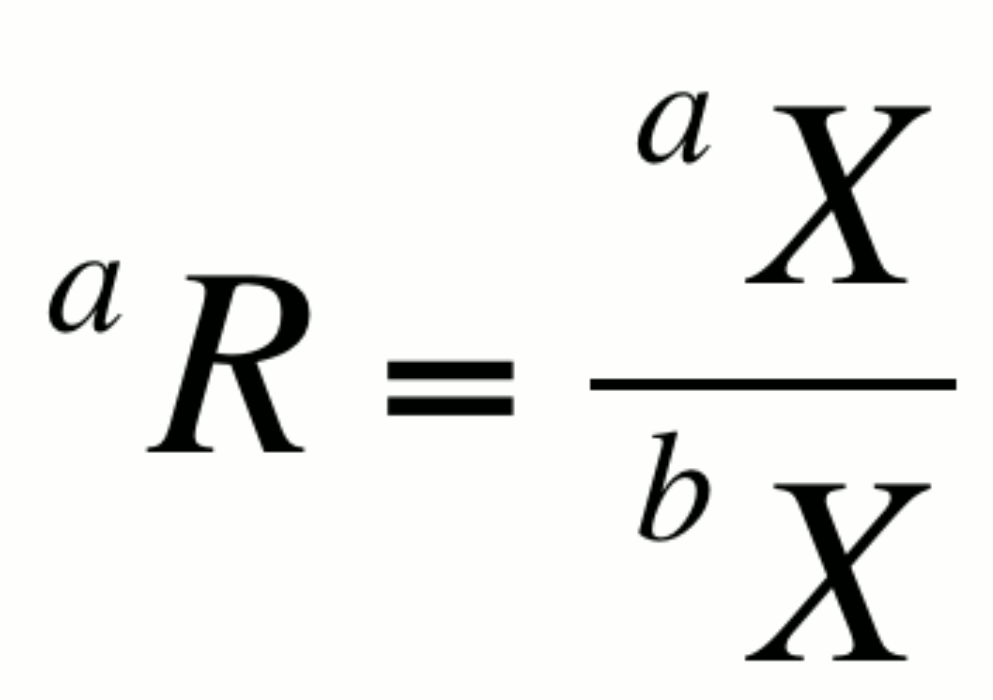
By convention, the more abundant isotope is placed in the denominator. This notation is not particularly helpful in itself however, as changes in R could result from changes in either ^aX or ^bX. It is however the basis for several expressions that are very useful.

Fractional abundance, ^aF:

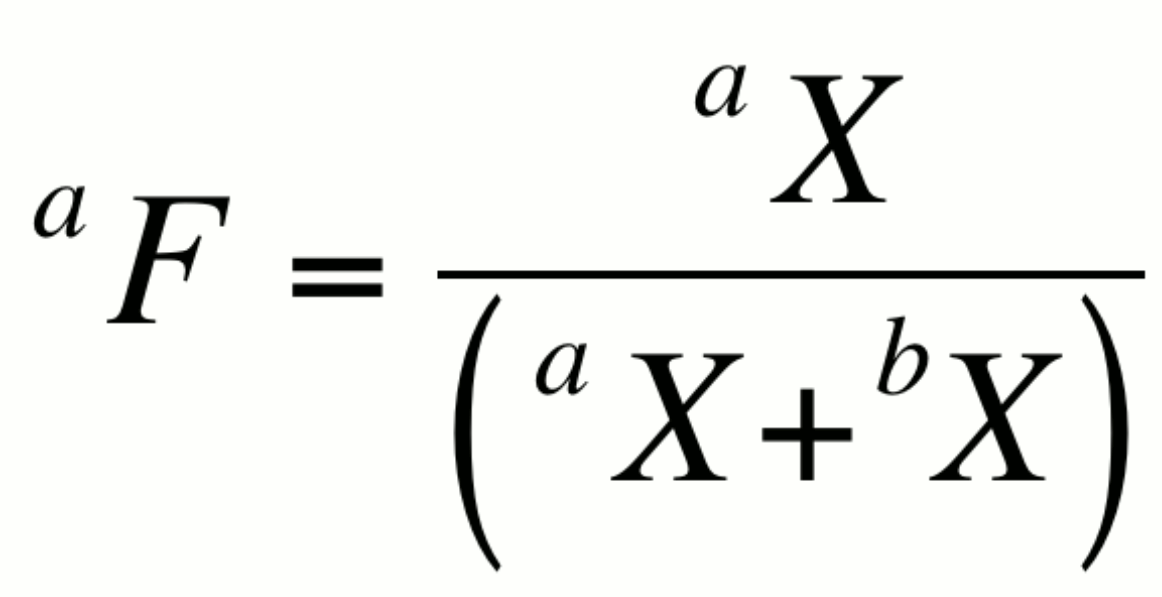
This expression is particularly useful in artificially enriched systems where the ratio of ^aX to ^bX is increased by the intentional addition of a pure source of one of the two isotopes (usually the heavy isotope).  The pure source is referred to as a spike, the process of adding the source as "spiking" a sample. Spikes allow us to monitor the movement of isotopes from one reservoir to another in response to one of more chemical reactions.
 

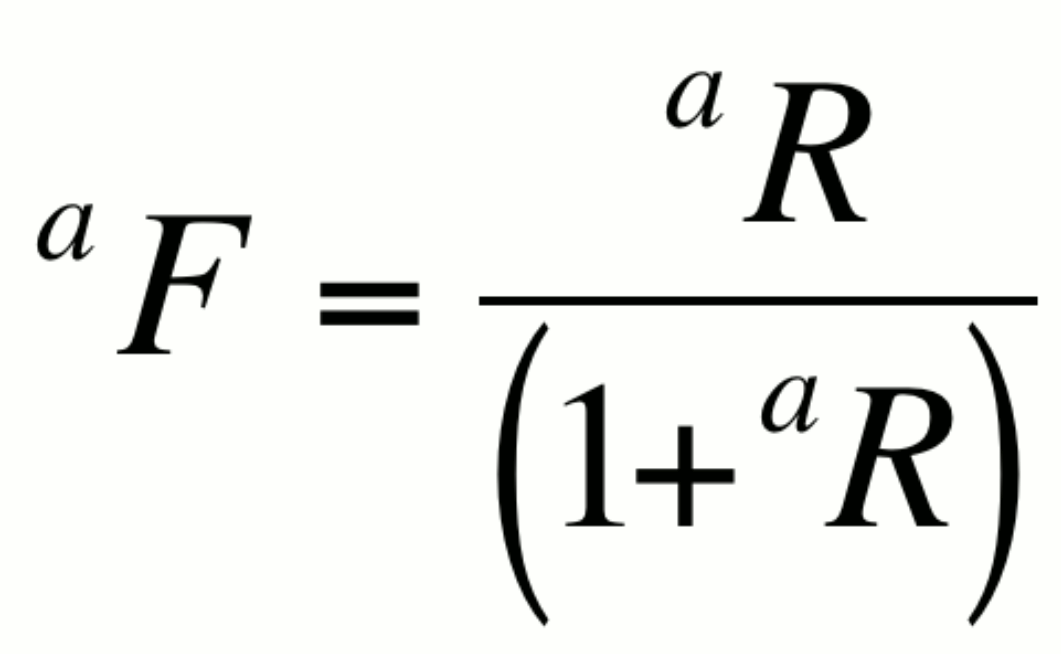Note that:  or alternatively,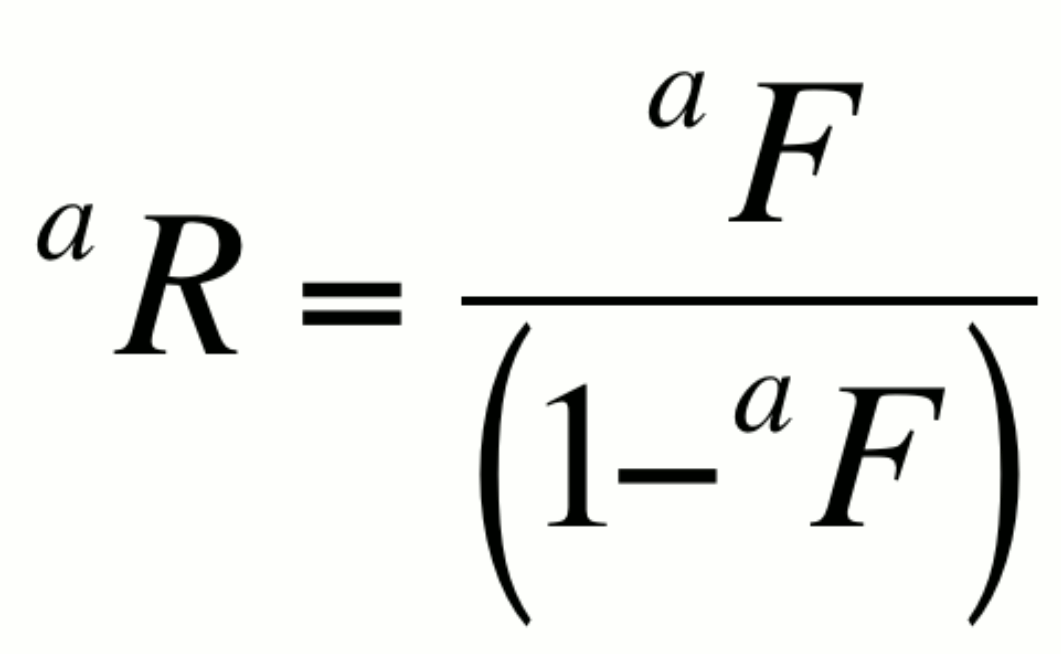 

 

The delta notation, d^aX.

In many natural systems, the isotopic ratio ^aR exhibits variability in the range of the third to fifth decimal place. Numbers this small are best presented in terms of per mil, or parts per thousand (‰).  The ratio in a sample, denoted here as ^aR_x can be expressed relative to the isotopic ratio of a standard ^aR_std using a difference relationship knows as the delta notation (d^aX):

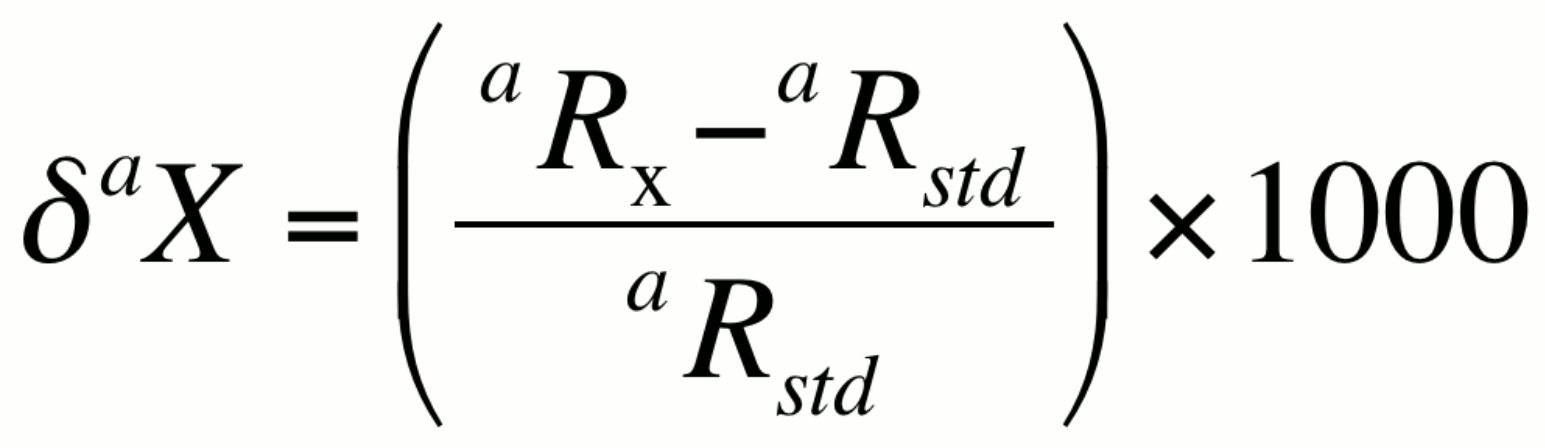  or alternatively,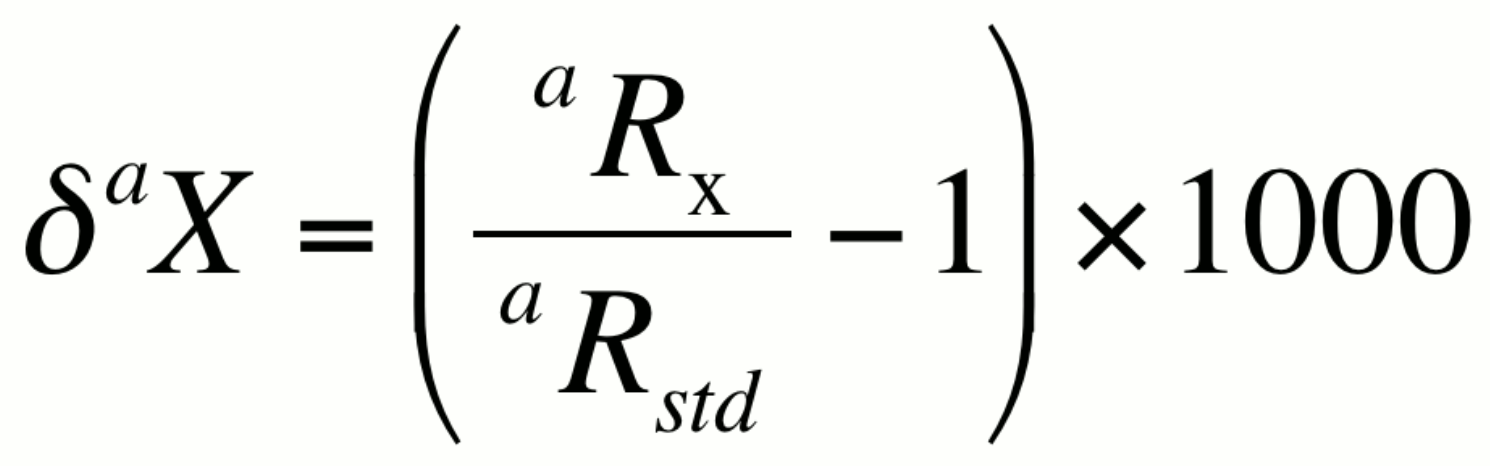 

Change of isotopic reference scale:
 

 

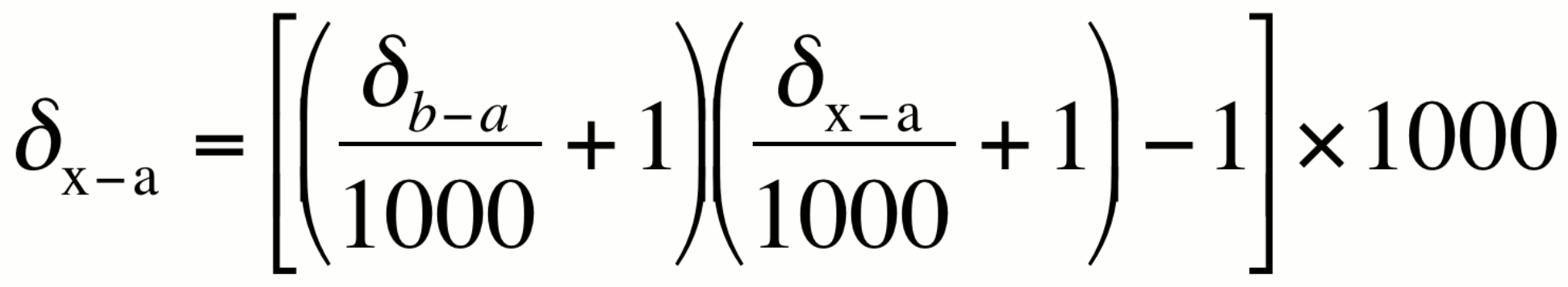
This relationship can be used to convert an isotopic value from one reference scale to another reference scale.

Measures of fractionation: a, 1000ln(a), e, and D

We are interested in measuring the isotopic offset between substances. Such offsets arise from the expression of an isotope effect due to equilibrium or kinetic fractionation during a physical process or chemical reaction. The size of this isotopic fractionation can be expressed in several ways.

The fractionation factor a is defined as:

 

 

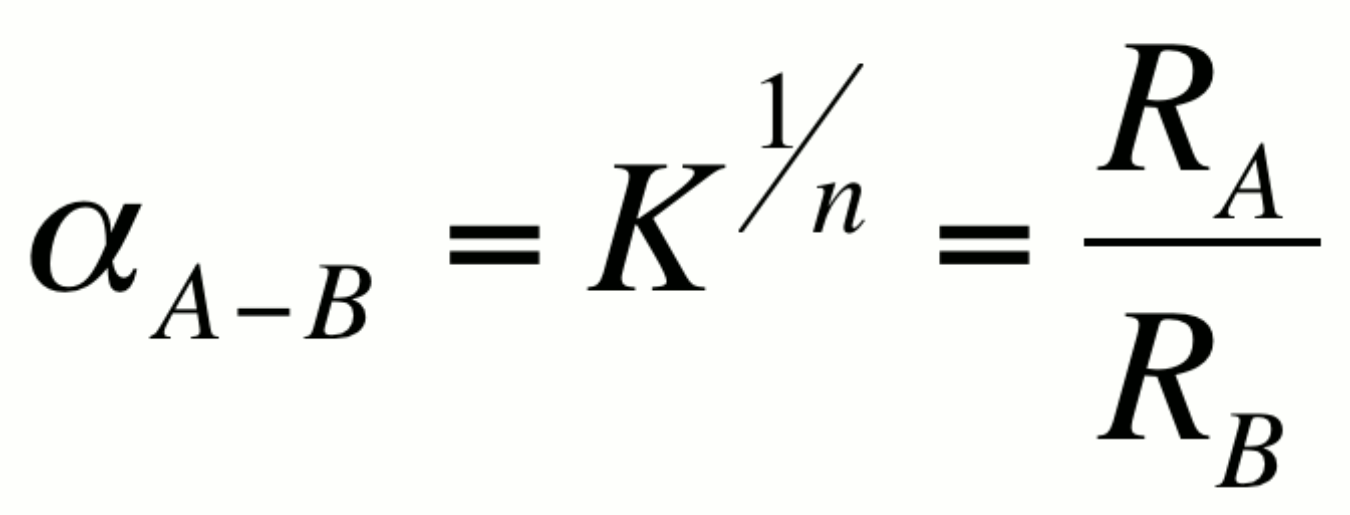
where K is the equilibrium constant for the associated reaction and n is the number of atoms exchanged. For simplicity, isotope exchange equations are usually written such that n=1 so that a =K.  It is worth noting that most values of a are close to 1, with variability in the third through fifth decimal place.  We can see that this is the case if we express a in terms of the delta notation

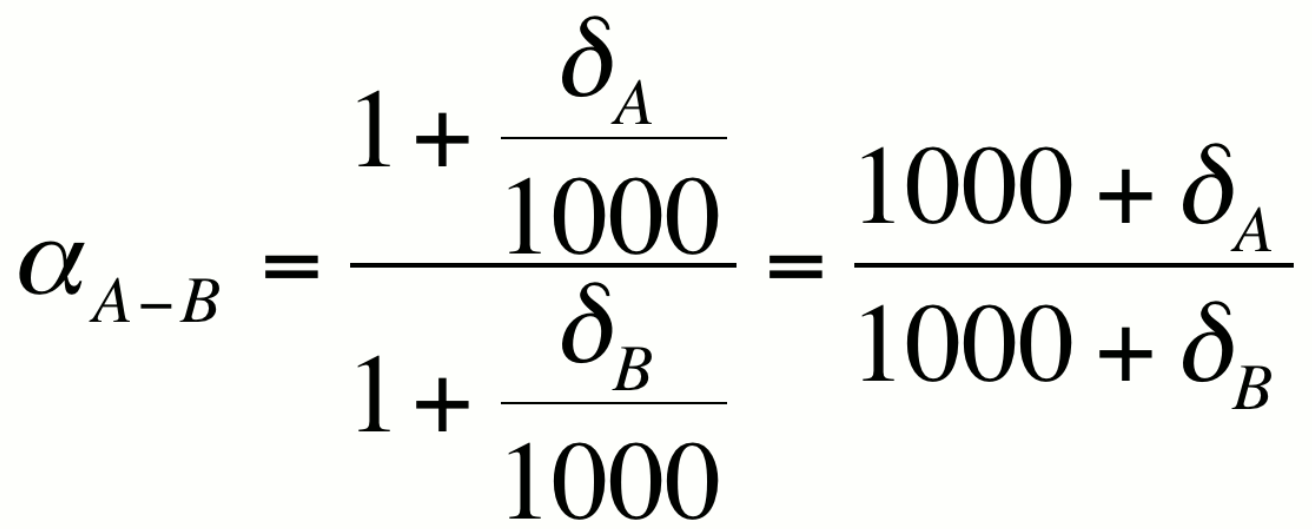
Because a is close to unity, it is convenient to express fractionation in ways that accentuate the differences between d_A and d_B. This can be done in one of three ways which yield approximately the same value for the per mil fractionation.

Natural log notation, 1000ln(a):

One would think that this notation would have its own symbol, but surprisingly, it does not! We can approximate the fractionation in per mil from the fractionation factor a by taking the natural log of a and multiplying it by 1000. This is written simply as 1000ln(a).  Mathematically, this works because we can think of a as being composed of 1 + e, a small deviation. Now if we take the natural log of 1+ e, the result can be expanded as a type of infinite series known as a Maclaurin series in which the first term e, is the largest and thus serves as a reasonable approximation of the natural log of a. If we retain more terms, we would obtain a more accurate result, but by convention, only the first term is retained:

Multiplying by 1000 yields the result in per mil. But since we are interested in e anyway, there is an easier way to express the per mil fractionation.

The epsilon notation, e:
 

The epsilon notation has the advantage over the 1000ln(a) notation in that it is an exact expression of the per mil fractionation. There is a final way of determining the per mil fractionation. This last method is the least accurate, but most commonly applied because of its simplicity.