![]()
Vertex Cover
![]()
![]()
![]()
Definition: A vertex-cover of an undirected graph G=(V, E) is a subset of V`subset of V such that if edge (u, v) is an edge of G then either u in V or v in V` (or both).
Problem: Find a vertex-cover of maximum size in a given undirected graph.
This optimal vertex-cover is the optimization version of an NP-complete problem but it is not too hard to find a vertex-cover that is near optimal.
APPROX-VERTEX_COVER (G: Graph)
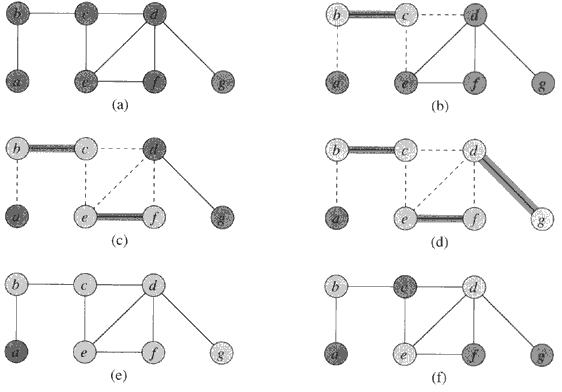
It is easy to see that the running time of this algorithm is O(V+E), using adjacency list to represent E`.
Theorem: APPROX-VERTEX-COVER is a polynomial-time 2-approximate algorithm i.e., the algorithm has a ration bound of 2.
Goal: Since this a minimization problem, we are interested in smallest possible c/c*. Specifically we want to show c/c* ≤ 2 = p(n). In other words, we want to show that APPROX-VERTEX-COVER algorithm returns a vertex-cover that is atmost twice the size of an optimal cover.
Proof: Let the set c and c* be the sets output by APPROX-VERTEX-COVER and OPTIMAL-VERTEX-COVER respectively. Also, let A be the set of edges selected by line 4.
Because, we have added both vertices, we get c = 2|A| but OPTIMAL-VERTEX-COVER would have add one of two.
=> c/c* ≤ p(n) = 2.
Formally, since no two edge in A are covered by the same vertex from c* (since, once an edge is picked in line 4, all other edges that are incident on its endpoints are deleted from E` in line 6) and we the lower bound:
|c*| ≥ A ---------------------------------- 1
On the size of an OPTIMAL-VERTEX-COVER.
In line 4, we picked both en points yielding an upper bound on the size of Vertex-Cover.
|c| ≤ 2|A|
Since, upper bound is an exact in this case, we have
|c|
= 2|A|
---------------------------------- 2
Take |c|/2 = |A| and put it in equation 1
|c*| ≥ |c|/2
|c*|/|c| ≥ 1/2
|c*|/|c| ≤ 2 = p(n)
proving the theorem. □