![]()
Euler Tour
![]()
![]()
![]()
The motivation of this section is derived from the famous Konigsberg bridge problem solved by Leonhard Euler in 1736. The 18th century German city of Königsberg was situated on the river Pregel. Within a park built on the banks of the river, there were two islands joined by seven bridges. The puzzle asks whether it is possible to take a tour through the park, crossing each bridge only once.
An exhaustive search requires starting at every possible point and traversing all the possible paths from that point - an O(n!) problem. However Euler showed that an Eulerian path existed if and only if
It is easy to see that these are necessary conditions: to complete the tour, one needs to enter and leave every point except the start and end points. The proof that these are sufficient conditions may be found in the literature . Thus we now have a O(n) problem to determine whether a path exists.
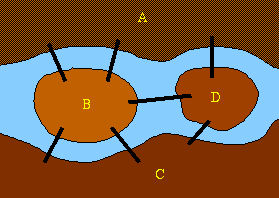
In order to get a solution transform the map into a graph in
which the nodes represent the "dry land" points and the arcs represent the
bridges.
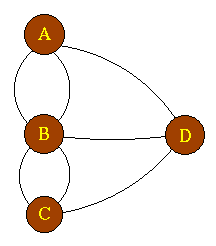
We can now easily see that the Bridges of Königsberg does not have a solution. A quick inspection shows that it does have a Hamiltonian path.
Definition A Euler tour of a connected, directed graph G = (V, E) is a cycle that traverses each edge of graph G exactly once, although it may visit a vertex more than once.
In the first part of this section we show that G has an Euler tour if and only if in-degrees of every vertex is equal to out-degree vertex. In the second part, we describe an algorithm to find an Euler tour of graph if one exists.
Part 1 Show that G has an Euler tour if and only if in-degree(v) = out-degree(v) for each vertex vÎV
Proof
First we'll work with => direction.
We will call a cycle simple if it visits each vertex no more than once, and complex if can visit a vertex more than once. We know that each vertex in a simple cycle in-degree and out-degree one, and any complex cycles can be expressed as a union of simple cycles. This implies that any vertex in a complex cycle (and in particular an Euler tour) has in-degree equal to its out-degree. Thus, if a graph has an Euler tour than all of its vertices have equal in- and out- degrees.
Now look at the <= direction.
Suppose we have a connected graph for which the in-degree and out-degree of all vertices are equal. Let C be the longest complex cycle within G. If C is not an Euler tour, then there is a vertex v of G touched by C such that not all edges in and out v of are exhausted by C. We may construct a cycle C` in G-C starting and ending at v by performing a walk in G-C. (The reason is that G-C also has a property that in-degrees and out-degrees are equal.) this simply means that the complex cycle that starts at v goes along the edges of C` (returning to v) and then goes along the edges of C is a longer complex cycle than C. This contradicts our choice of C as the longest complex cycle which means that C must have been an Euler tour.
Part 2 Find an Euler tour of given graph G if one exists.
ALGORITHM
Given a starting vertex , the v0 algorithm will first find a cycle C starting and ending at v0 such that C contains all edges going into and out of v0. This can be performed by a walk in the graph. As we discover vertices in cycle C, we will create a linked list which contains vertices in order and such that the list begins and ends in vertex v0. We set the current painter to the head of the list. We now traverse the list by moving our pointer "current" to successive vertices until we and a vertex which has an outgoing edge which has not been discovered. (If we reach the end of the list, then we have already found the Euler tour). Suppose we find the vertex, vi, that has an undiscovered outgoing edge. We then take a walk beginning and ending at vi such that all undiscovered edges containing vi are contained in the walk. We insert our new linked list into old linked list in place of vi and more "current" to the new neighbor pointed to the first node containing vi. We continue this process until we search the final node of the linked list, and the list will then contains an Euler tour.
The algorithm traverse each edge at most twice, first in a walk and second while traversing the list to find vertices with outgoing edges. Therefore, the total running time of the algorithm is O(|E|).