
Sets

A
set is a collection of different things (distinguishable objects or distinct objects)
represented as a unit. The objects in a set are called its elements or
members. If an object x
is a member of a set S, we write x  S. On the the hand, if x is not a member of S, we write z
S. On the the hand, if x is not a member of S, we write z 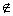 S. A
set cannot contain the same object more than once, and its elements are
not ordered.
S. A
set cannot contain the same object more than once, and its elements are
not ordered.
For example, consider the set S= {7, 21, 57}.
Then 7  {7, 21,
57} and 8
{7, 21,
57} and 8 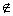 {7, 21, 57} or equivalently, 7
{7, 21, 57} or equivalently, 7
 S and 8
S and 8 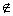 S.
S.
We can also describe a set containing elements according to some rule.
We write
{n : rule about n}
Thus, {n : n = m2 for some m  N } means that a set of perfect squares.
N } means that a set of perfect squares.
Set Cardinality
The number of elements
in a set is called cardinality or size of the set, denoted |S|
or sometimes n(S). The two sets have same cardinality if their elements
can be put into a one-to-one
correspondence. It is easy to see that the cardinality of an
empty set is zero i.e., |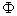 |
.
|
.
Mustiest
If we do want to take the number
of occurrences of members into
account, we call the group a multiset.
For example, {7} and {7, 7} are identical as set but {7} and {7, 7} are
different as multiset.
Infinite
Set
A set contains infinite elements. For example, set
of negative
integers, set of integers, etc.
Empty
Set
Set contain no member, denoted as 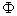 or {}.
or {}.
Subset
For two sets A and B, we say that A is a subset of B, written A 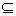 B, if every member
of A also is a member of B.
B, if every member
of A also is a member of B.
Formally, A 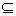 B if
B if
x  A implies x
A implies x  B
B
written
x  A => x
A => x  B.
B.
Proper Subset
Set A is a proper subset of B, written A 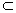 B, if A is a subset
of B and not equal to
B. That is, A set A is proper subset of B
if A
B, if A is a subset
of B and not equal to
B. That is, A set A is proper subset of B
if A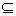 B but A
B but A 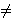 B.
B.
Equal Sets
The sets A and B are equal, written A = B, if each is a subset of the
other. Rephrased definition, let A and B be sets. A = B if A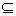 B and B
B and B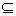 A.
A.
Power
Set
Let A be the set. The power of A, written P(A) or 2A, is the
set of all subsets of A. That is, P(A) = {B : B 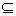 A}.
A}.
For example, consider A={0, 1}. The power set of A is {{}, {0}, {1},
{0, 1}}. And the power set of A is the set of all pairs (2-tuples)
whose elements
are 0 and 1 is {(0, 0), (0, 1), (1, 0), (1, 1)}.
Disjoint Sets
Let A and B be sets. A and B are disjoint if A B
=
B
= 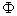 .
.
Union of Sets
The union of A and B, written A B, is the set we get by combining all elements in A and B into a single
set. That is,
B, is the set we get by combining all elements in A and B into a single
set. That is,
For two finite sets A and B, we have identity
|A B|
= |A| + |B| - |A
B|
= |A| + |B| - |A B|
B|
We can conclude
|A B|
B|
 |A| + |B|
|A| + |B|
That is,
if |A B|
= 0 then |A
B|
= 0 then |A B|
= |A| + |B| and if A
B|
= |A| + |B| and if A 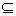 B then |A|
B then |A|  |B|
|B|
Intersection Sets
The intersection of set set A and B, written A B, is the set of
elements that are both in A and in B. That is,
B, is the set of
elements that are both in A and in B. That is,
Partition
of Set
A collection of S = {Si} of nonempty sets form a partition of a set if
i. The set are pair-wise disjoint, that is,
Si, Sj  and i
and i 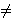 j imply Si
j imply Si  Sj =
Sj = 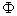 .
.
ii. Their union is S, that is, S =  Si
Si
In other words, S form a partition of S if each element of S appears in
exactly on Si.
Difference of Sets
Let A and B be sets. The difference of A and B is
A - B = {x :
x  A and x
A and x 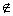 B}.
B}.
For example, let A = {1, 2, 3} and B = {2, 4, 6, 8}. The set difference
A - B = {1, 3} while B-A = {4, 6, 8}.
Complement
of a Set
All set under consideration are subset of some large set U called universal set. Given a
universal set U, the complement of A, written A', is the set of all
elements under
consideration that are not in
A.
Formally, let A be a subset of universal set U. The complement of A in
U is
A' = A - U
OR
A' = {x : x  U and x
U and x 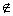 A}.
A}.
For any set A 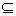 U, we have following laws
U, we have following laws
i.
A'' = A
ii. A  A' =
A' = 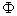 .
iii. A
.
iii. A  A' = U
A' = U
Symmetric difference
Let A and B be sets. The symmetric difference of A and B is
A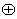 B = { x : x
B = { x : x  A or x
A or x  B but not both}
B but not both}
Therefore,
As an example, consider the following two sets A = {1, 2, 3} and B =
{2, 4, 6, 8}. The symmetric difference, A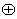 B = {1, 3, 4, 6, 8}.
B = {1, 3, 4, 6, 8}.
Sequences
A sequence of objects is a list of objects in some order. For example,
the sequence 7, 21, 57 would be written as (7, 21, 57). In a set the
order does not matter but in a sequence it does.
Hence, (7, 21, 57) 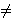 {57, 7, 21} But (7, 21, 57) = {57, 7, 21}.
{57, 7, 21} But (7, 21, 57) = {57, 7, 21}.
Repetition
is not permitted in a
set but repetition is permitted in a sequence. So, (7, 7, 21, 57) is different from {7, 21, 57}.
Tuples
Finite sequence often are called tuples. For example,
(7, 21)
2-tuple or pair
(7, 21, 57) 3-tuple
(7, 21, ..., k ) k-tuple
An ordered pair of two elements a and b is denoted (a, b) and can be
defined as (a, b) = (a, {a, b}).
Cartesian Product or Cross Product
If A and B are two sets, the cross product of A and B, written A×B, is the set of all pairs
wherein the first element is a member of the set A and the second
element is a member of the set B. Formally,
A×B = {(a, b) :
a  A, b
A, b  B}.
B}.
For example, let A = {1, 2} and B = {x, y, z}. Then A×B =
{(1, x), (1, y), (1, z), (2, x), (2, y), (2, z)}.
When A and B are finite sets, the cardinality of their product
is
|A×B| = |A| . |B|
n-tuples
The cartesian product of n sets A1, A2, ..., An
is the set of n-tuples
A1 × A2 × ... × An = {(a1, ..., an) : ai  Ai,
i = 1, 2, ..., n}
Ai,
i = 1, 2, ..., n}
whose cardinality is
|
A1 × A2 × ... × An|
= |A1| . |A2| ... |An|
If all sets are finite. We denote an n-fold cartesian product over
a single set A by the set
An
= A
× A × ... × A
whose cardinality is
|An |
= | A|n
if A is finite.


![]()
![]()
![]()
![]()
 S. On the the hand, if x is not a member of S, we write z
S. On the the hand, if x is not a member of S, we write z 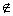 S. A
set cannot contain the same object more than once, and its elements are
not ordered.
S. A
set cannot contain the same object more than once, and its elements are
not ordered. {7, 21,
57} and 8
{7, 21,
57} and 8 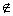 {7, 21, 57} or equivalently, 7
{7, 21, 57} or equivalently, 7
 S and 8
S and 8 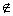 S.
S. N } means that a set of perfect squares.
N } means that a set of perfect squares.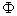 |
.
|
. 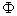 or {}.
or {}. 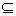 B, if every member
of A also is a member of B.
B, if every member
of A also is a member of B. 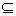 B if
B if A implies x
A implies x  B
B A => x
A => x  B.
B.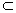 B, if A is a subset
of B and not equal to
B. That is, A set A is proper subset of B
if A
B, if A is a subset
of B and not equal to
B. That is, A set A is proper subset of B
if A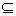 B but A
B but A 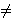 B.
B.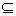 B and B
B and B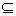 A.
A.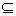 A}.
A}. B
=
B
= 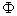 .
. B, is the set we get by combining all elements in A and B into a single
set. That is,
B, is the set we get by combining all elements in A and B into a single
set. That is, B
= { x : x
B
= { x : x  A or
x
A or
x  B}.
B}. B|
= |A| + |B| - |A
B|
= |A| + |B| - |A B|
B| B|
B|
 |A| + |B|
|A| + |B| B|
= 0 then |A
B|
= 0 then |A B|
= |A| + |B| and if A
B|
= |A| + |B| and if A 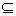 B then |A|
B then |A|  |B|
|B| B, is the set of
elements that are both in A and in B. That is,
B, is the set of
elements that are both in A and in B. That is, B = { x : x
B = { x : x  A and
x
A and
x  B}.
B}. and i
and i 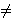 j imply Si
j imply Si  Sj =
Sj = 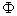 .
. Si
Si A and x
A and x 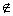 B}.
B}. U and x
U and x 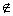 A}.
A}.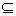 U, we have following laws
U, we have following laws A' =
A' =  .
. A' = U
A' = U B = { x : x
B = { x : x  A or x
A or x  B but not both}
B but not both} B = (A
B = (A B)
- (A
B)
- (A B)
B)  B = {1, 3, 4, 6, 8}.
B = {1, 3, 4, 6, 8}. {57, 7, 21} But (7, 21, 57) = {57, 7, 21}.
{57, 7, 21} But (7, 21, 57) = {57, 7, 21}. A, b
A, b  B}.
B}. Ai,
i = 1, 2, ..., n}
Ai,
i = 1, 2, ..., n}