![]()
Graph Planarity
![]()
![]()
![]()
A graph G is planar if it can be drawn in the plane in such a way that no two edges meet each other except at a vertex to which they are incident. Any such drawing is called a plane drawing of G.
For example, the graph K4 is planar, since it can be drawn in the plane without edges crossing.
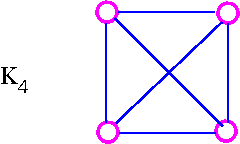
The three plane drawings of K4 are:
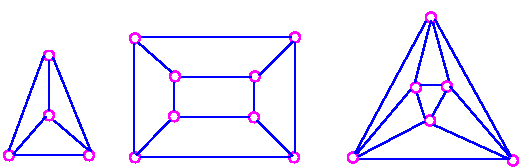
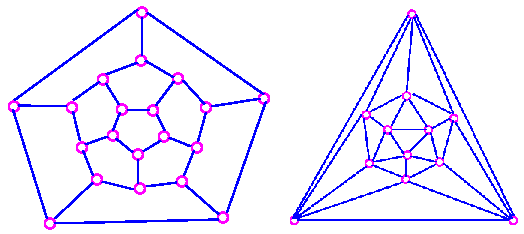
The five Platonic graphs are all planar.
On the other hand, the complete bipartite graph K3,3 is not planar, since every drawing of K3,3 contains at least one crossing. why? because K3,3 has a cycle which must appear in any plane drawing.
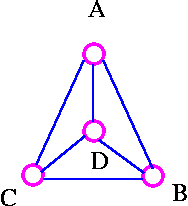
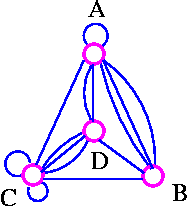
To study planar graphs, we restrict ourselves to simple graphs.
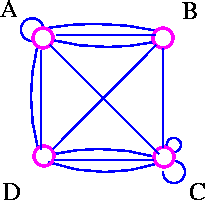
Remove loops and multiple edge.
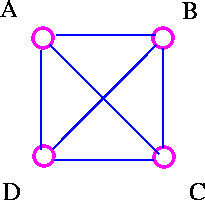
Draw without multiple edge.
Insert loops and multiple edges.
Euler's Formula
If G is a planar graph, then any plane drawing of G divides the plane into regions, called faces. One of these faces is unbounded, and is called the infinite face. If f is any face, then the degree of f (denoted by deg f) is the number of edges encountered in a walk around the boundary of the face f. If all faces have the same degree (g, say), the G is face-regular of degree g.
For example, the following graph G has four faces, f4 being the infinite face.
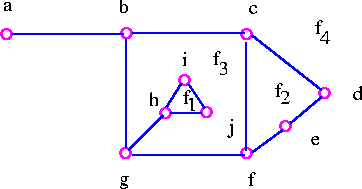
It is easy to see from above graph that deg f1=3, deg f2=4, deg f3=9, deg f4=8.
Note that the sum of all the degrees of the faces is equal to twice the number of edges in the the graph , since each edge either borders two different faces (such as bg, cd, and cf) or occurs twice when walk around a single face (such as ab and gh). The Euler's formula relates the number of vertices, edges and faces of a planar graph. If n, m, and f denote the number of vertices, edges, and faces respectively of a connected planar graph, then we get n-m+f = 2.
The Euler formula tells us that all plane drawings of a connected planar graph have the same number of faces namely, 2+m-n.
Theorem 1 (Euler's Formula) Let G be a connected planar graph, and let n, m and f denote, respectively, the numbers of vertices, edges, and faces in a plane drawing of G. Then n - m + f = 2.
Proof We employ mathematical induction on edges, m. The induction is obvious for m=0 since in this case n=1 and f=1. Assume that the result is true for all connected plane graphs with fewer than m edges, where m is greater than or equal to 1, and suppose that G has m edges. If G is a tree, then n=m+1 and f=1 so the desired formula follows. On the other hand, if G is not a tree, let e be a cycle edge of G and consider G-e. The connected plane graph G-e has n vertices, m-1 edges, and f-1 faces so that by the inductive hypothesis,
n - (m - 1) + (f - 1) = 2
which implies that
n - m + f = 2.
We can obtains a number of useful results using Euler's formula. (A "corollary" is a theorem associated with another theorem from which it can be easily derived.)
Corollary 1 Let G be a connected planar simple graph with n vertices, where n ≥ 3 and m edges. Then m ≤ 3n - 6.
Proof For graph G with f faces, it follows from the handshaking lemma for planar graph that 2m ≥ 3f (why?) because the degree of each face of a simple graph is at least 3), so f ≤ 2/3 m.
Combining this with Euler's formula
Since n - m + f = 2
We get m - n + 2 ≤ 2/3 m
Hence m ≤ 3n - 6.
As an example of Corollary 1, show that K5 is non-planar.
Proof Suppose that K5 is a planar graph. Since K5 has 5 vertices and 10 edges it follows from Corollary 1 that 10 (3 × 5) - 6 = 9. This contradiction shows that K5 is non planar.
It is important to note that K3,3 has 6 vertices and 9 edges, and it is true that 9 ≤ (3 × 6) - 6 = 12. This fact simply shows that we cannot use Corollary 1 to prove that K3,3 is non-planar. This leads us to following corollary.
Corollary 2 Let G be a connected planar simple graph with n vertices and m edges, and no triangles. Then m ≤ 2n - 4.
Proof For graph G with f faces, it follows from the handshaking lemma for planar graphs that 2m ≥ 4f (why because the degree of each face of a simple graph without triangles is at least 4), so that f ≤ 1/2 m.
Combining this with Euler's formula
Since n - m + f = 2
Implies m -n + 2 = f
We get m - n + 2 ≤ 1/2m
Hence
m ≤ 2n - 4
As an example of Corollary 2, show that K3,3 is non-planar.
Proof Suppose that K3,3 is a planar graph. Since K3,3 has 6 vertices and 9 edges and no triangles, it follows from Corollary 2 that 9 ≤ (2×6) - 4 = 8. This contradiction shows that K3,3 is non-planar.
Corollary 3 Let G be a connected planar simple graph. Then G contains at least one vertex of degree 5 or less.
Proof From Corollary 1, we get m ≤ 3n-6. Suppose that every vertex in G has degree 6 or more. Then we have 2m ≥ 6n (why? because 2m is the sum of the vertex-degree), and therefore m≥3n. This contradiction shows that at least one vertex has degree 5 or less.
Now we will show by using Euler's formula that there are only five regular convex polyhedra - namely, the tetrahedron, cube, octahedron, dodecahedron, and isosahedron.
Theorem 2 There are only 5 regular convex polyhedra.
Proof We prove this theorem by showing that there are only 5 connected planar graph G with following properties.
Let n, m and f be the numbers of vertices, edges, and faces of such a planar graph G. Then, from properties (i) and (ii), we ge
m = 1/2 dn
= 1/2 gf
This gives us n = 2m/d and f = 2m/g
Here Euler's formula (n - m + f = 2) holds, since G is a planar graph.
Therefore, 2m/d - m + 2m/g = 2
Which can be written as
1/d - 1/2 + 1/g = 1/m
Since 1/m > 0, it follows that 1/d + 1/g > 1/2
Note that each of d and g is at least 3, so each of
1/d and 1/g is at most
1/3.
Therefore,
1/d > 1/2 - 1/3 = 1/6 and
1/g > 1/2 - 1/3 = 1/6.
and we conclude that d < 6 and g < 6.
This means that the only possible values of d and g are 3, 4, and 5. However, if both d and g are greater than 3, then
1/d + 1/g ≤ 1/4 + 1/4 = 1/2
which is a contradiction. This leaves us with just five cases:
Case 1: When
d = 3 and
g = 3.
we get 1/m = 1/3 - 1/2 + 1/3 = 1/6
Therefore m = 6
It follows that n = 8
and f = 4
and this gives the Tetrahedron.
Case 2: When d = 3
and g = 4.
we get 1/m = 1/3 - 1/2 + 1/4 = 1/12
Therefore m = 12
It follows that n = 8
and f = 6
and this gives the Cube.
Case 3: When d = 3
and g = 5.
we get 1/m = 1/3 - 1/2 + 1/5 = 1/30
Therefore m = 30
It follows that n = 20
and f = 12
and this gives the Dodecahedron.
Case 4: When d = 4
and g = 3.
we get 1/m = 1/4 - 1/2 + 1/3 = 1/12
Therefore m = 12
It follows that n = 6
and f = 8
and this gives the Octahedron.
Case 5: When d = 5
and g = 3.
we get 1/m = 1/5 - 1/2 + 1/3 = 1/30
Therefore m = 30
It follows that n = 12
and f = 20
and this gives the Icosahedron.
And this completes the proof.
Planarity Testing
The Corollaries 1, 2 and their generalization are often useful for showing that graph is not planar. Unfortunately, there are many graphs which satisfy these inequalities but are not planar. Therefore, we need other way to decide planarity.
Some important observations:
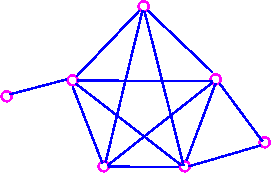
- Since it contains K5 as a subgraph.
- The following graph is also non-planar
- Since the it contains K3,3 as a subgraph.
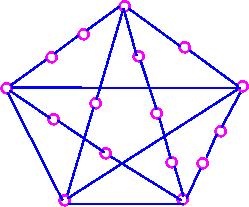
- Since it is a subdivision of K5.
- Also, the following graph is non-planar,
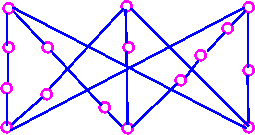
- Since it is a subdivision of K3,3.
It follows from observations (2a) and (3a) that, if any graph G contains a subdivision of K5 and K3,3 as a subgraph, then G must be non-planar.
Why are we so obsessed with K5 and K3,3? The reason is that all non-planar graphs can be obtained by adding vertices and edges to a subdivision of K5 and K3,3.
Every non-planar graph contains K5 or K3,3 as a subgraph.
Following result is due to the Polish mathematician K. Kuratowski.
Theorem 3 A graph is planar if and only if it does not contain a subdivision of K5 and K3,3 as a subgraph.
Graph Contraction
In the following figure contradiction is done by bringing the vertex w closer and closer to v until w and v coincide and then coalescing multiple edges into a single edge.
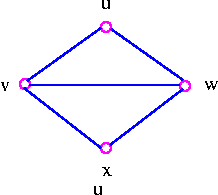
Bring vertex w closer to v.
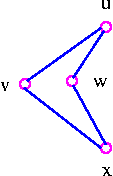
Coalesce vertex v and vertex w.
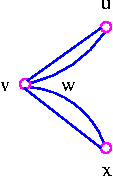
Finally, coalesce multiple edges and we have
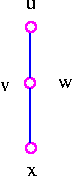
A contraction of a graph is the result of a sequence of edge-contractions. For example, K5 is a contraction of the Petersen graph
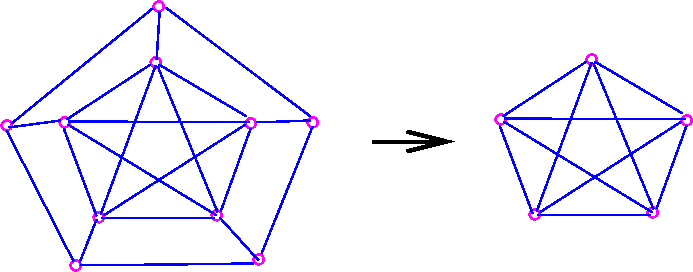
Theorem 4 A graph is planar if and only if it does not contain a subgraph which has K5 and K3,3 as a contraction.
The basic idea to test the planarity of the given graph is if we are able to
spot a subgraph which is a subdivision of K5 or K3,3 or a subgraph which
contracts to K5 or K3,3 then a given graph is non-planar.
Theorems 3 and 4 give us necessary and sufficient conditions for a graph to be planar in purely graph-theoretic sense (subgraph, subdivision, K3,3, etc) rather than geometric sense (crossing, drawing in the plane, etc). This is the reason, why there exists no algorithm uses these two theorems for testing the planarity of a graph. Since this would involve looking at a large number of subgraph and verifying that none of them is a subdivision of, or contracts toK5 or K3,3.
Duality
Given a connected planar graph G, we construct dual graph G* in three stages.
This procedure is illustrated as follows:
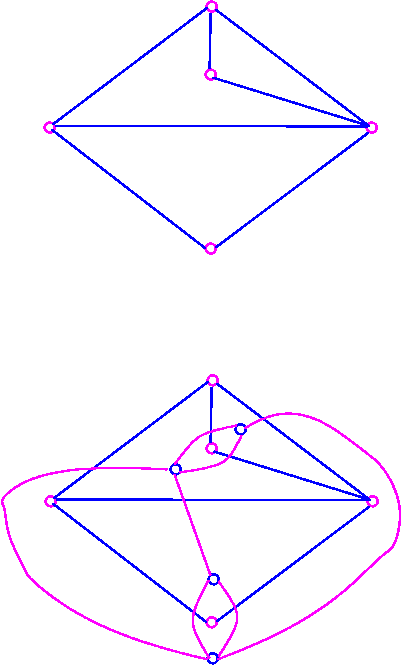
Note that each plane drawing of G given rise to just one dual graph G*.
Following theorem illustrates a simple relationship between the number of vertices, faces and edges of a graph and its dual.
Theorem 6 If G is a connected planar graph with n vertices, f faces and m edges, then G* has f vertices, n faces and m edges.
In the above example, G has 5 vertices, 4 faces and 7 edges, and G* has 4 faces, 5 faces, and seven edges.
Note that if G is a connected planar graph, then G* is also connected planar graph.
![]()