Given n points in the plane, find a largest circle that contains no points of the set and whose center is internal to the convex hull of those points.

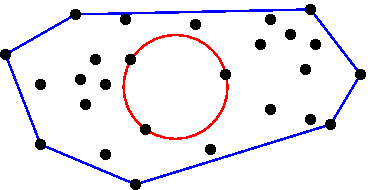
An early solution of the problem is an algorithm whose worst-case running time is O(n3) [1]. Preparata and Shomos [2] showed that is problem can be solved in O(nlogn) time with the help of Voronoi diagram. The O(nlogn) solution is optimal for this problem.

The algorithm for this problem used the following property of the Voronoi diagram: For every Voronoi vertex, there exists a unique circle centered at that vertex and passes through three or more sites.

Reference

[1]    B. Dasarathy and L. J. White, "On some maximin location of classifier problems", Computer Science Conference, Washington, D.C., 1975 (Unpublished lecture).

[2]    F.P. Preparata and M.I. Shamos, "Computational Geometry", Springer-Verlag, 1985.