[Bistable Nematic
(BiNem) mode mode]
The BiNem mode was introduced by Nemoptic, it uses two different
anchoring conditions on two substrates to achieve the bistability, usually one
substrate is a weak planar anchoring and the other one has a strong
tilted anchoring. This is also called "surface
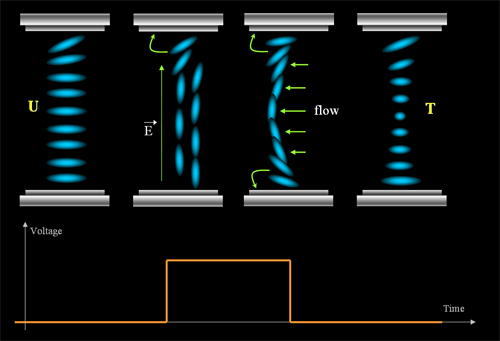
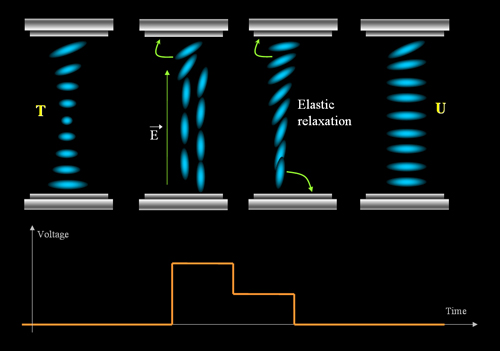
anchoring breaking". The BiNem mode has two states, which are
uniform (U) and twist (T) states. The two states can be interchanged
by applying different pulses. As shown in the following figure, to
switch from U state to the T state, a pulse with sharp falling edge
is required. while from T to U state, a pulse with smooth falling
edge is necessary. Both the U and T states are stable even without
applied field.
 (a)
(a)
 (b)
(b)
Figure 1. BiNem
display working principle (a) pulse with a sharp falling edge; (b) pulse with a
smooth falling edge.
In principle, the BiNem only has two states, and hence no gray scales. But it
can be realized by driving signal modulation, through controlling the amount of
black and white area separated by a border line in one pixel. When the signal
changes, the border line moves to change the amount of black and white, hence
different gray scales are achieved. Since it is like the curtain moving down on
a window, it is also called "curtain effect".
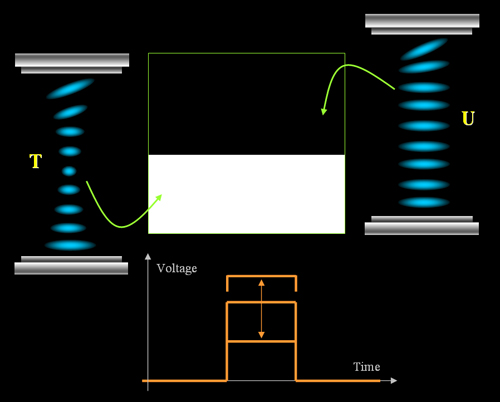
Figure 2. Gray-scale realization
in BiNem display by "curtain effect".
The color BiNem display is
realized by implementing standard color filters. A 32K color display was
demonstrated by Nemoptic*.

(*Picture is
from nemoptic.com)
Further Readings
and References:
I. Dozov et al, Fast bistable nematic display from coupled
surface anchoring breaking , Proceedings of SPIE vol. 3015, 61
(1997).
I. Dozov et al., Fast bistable nematic display using monostable
surface switching , Appl. Phys. Lett. 70, 1179 (1997).
D. N. Stoenescu, I. Dozov, and Ph. Martinot-Lagarde, Mol.Cryst.
Liq. Cryst. Sci. Technol., Sect. A 351, 427 (2000).
S. Lamarque-Forget, Ph. Martinot-Lagarde, and I. Dozov, Jpn. J.
Appl. Phys., Part 2 40 L349 (2001).
S. Joly, K. Antonova, Ph. Martinot-Lagarde, and I. Dozov,
Phys. Rev. E 70, 050701(R) (2004)